2 - Etude d'un signal rectangulaire: sin(t) + sin(3t)/3 + sin(5t)/5 with a period of 2Pi
Dans cet exemple on utilise la méthode du Population Mean Cosinor (Un modèle global est calculé sur l'ensemble des séries
et on détermine la moyenne vectorielle) Ce type de modélisation est utilisé pour déterminer les caractéristiques d'une
population.
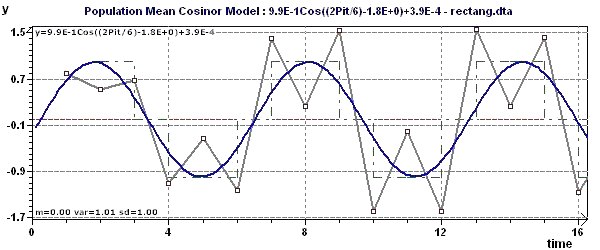
Figure 2-a : Une des périodes est 2Pi (6,28). Représentation du modèle, des points expérimentaux et de la courbe d'interpolation.
Figure 2-b : Population Mean Cosinor et tests associés sur le modèle global (Intervalle de confiance 95% α = 0.05) Résumé.
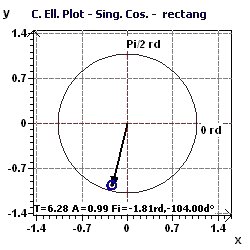
Figure 2-c : Période de 2Pi. Représentation de l'ellipse de confiance (p fixed 0.95, means confidence interval = 95%, α = 0.05) du Population Mean Cosinor selon
Gouthière and Jacquin (Plus la surface est petite plus la précision est grande sur la détermination de la période)
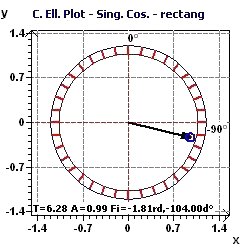
Figure 2-d : Période de 2Pi; Représentation de l'ellipse de confiance (p fixed 0.95, means confidence interval = 95%, α = 0.05) du Population Mean Cosinor selon
Nelson et Bingham (Plus la surface est petite plus la précision est grande sur la détermination de la période)
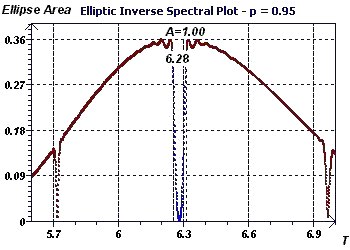
Figure 2-e : Période initiale de 2Pi. Le spectre elliptique inverse selon Gouthière permet de détecter les périodes. Ici on voit un minimum
à 6,28 pour un intervalle de confiance de 95% (α = 1-p) La partie en bleue correspond à la significativité de l'hypothèse nulle du test de l'ellipse.
En augmentant la probabilité on rétrécit l'intervalle de périodes valides.
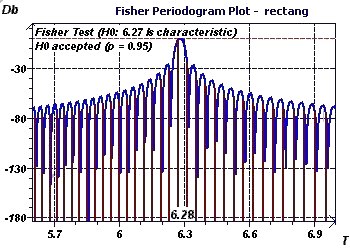
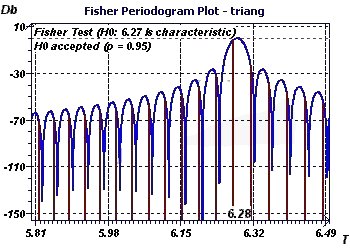
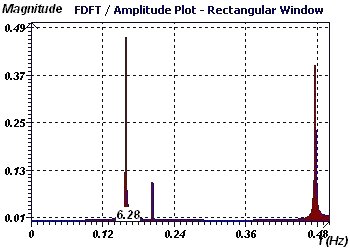
Figure 2-f : Période initiale de 2Pi. Périodogramme de Fisher (avec p = 0,95) permet de détécter une période et sa validité pour une
probabilité fiwée. Cette méthode qui est dérivée des DFT teste la fondamentale à 6,27 en utilisant une hypothèse nulle come quoi cette période est caractéristique du phénomène étudié.
L'analyse spectrale est moins intéressante que le périodogramme de Scargle ou l'Autopériodogramme selon Jenkins et Watts.
3 - Etude d'un signal en dents de scie: sin(t) + sin(2t)/2 + sin(3t)/3 avec un période de 2Pi.
Dans cet exemple, on utilise la méthodologie du Single Cosinor (Un modèle global est calculé sur un ensemble de points) Ce type
de modélisation est utilisé pour déterminer les caractéritisques d'un sujet.
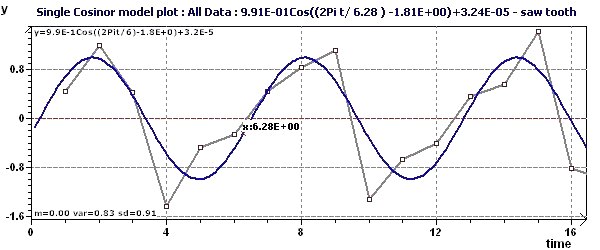
Figure 3-a : Une des périodes détectées est 2Pi (6,28). Représentation du modèle, des points expérimentaux et de la courbe d'interpolation.
Figure 3-b : Single Cosinor et tests associés sur le modèle (Intervalle de confiance 0,95)
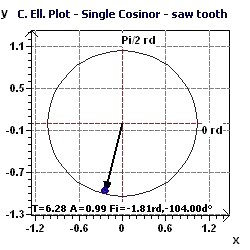
Figure 3-c : Période 2Pi. Représentation de l'ellipse de confiance selon Gouthière et Jacquin.
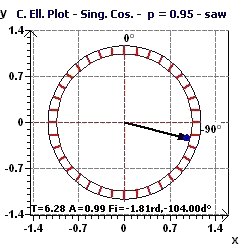
Figure 3-d : Period of 2Pi. Représentation de l'ellipse de confiance selon Nelson et Bingham.
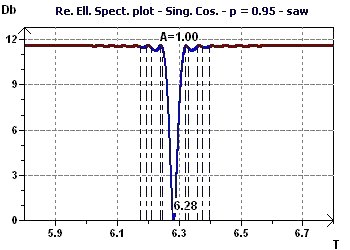
Figure 3-e : Le spectre elliptique inverse selon Gouthière présente un minimum à 6,28
(La partie bleue correspond à la significativité de l'hypothèse nulle du test de l'ellipse)
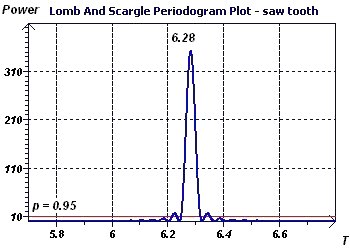
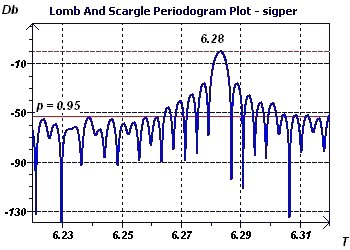
Figure 3-f : Le périodogramme de Scargle met en évidence la période de 6,28 de manière identique à celui utilisé précedemment.
4 - Etude d'un signal triangulaire: sin(t) - sin(3t)/3² + sin(5t)/5² de période 2Pi
Dans cet exemple, nous montrons différentes méthodes pour détecter les périodes comparées au spectre elliptique inverse (RES) selon Gouthière
(La bonne qualité des données permet de trouver des résultats précis. Ce n'est pas toulours le cas)
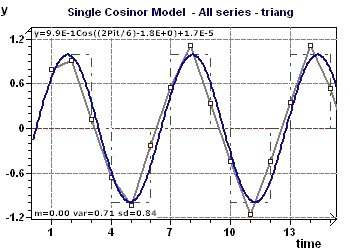
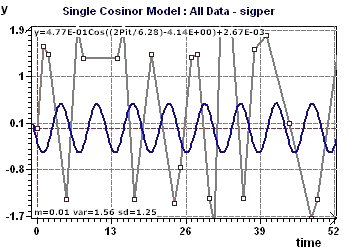
Figure 4-a : Une des période détectées est 2Pi (6,28) Représentation du modèle et des points expérimentaux.
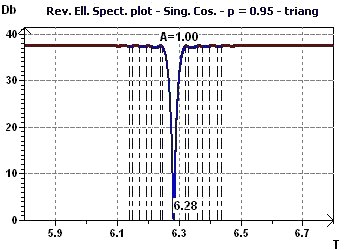
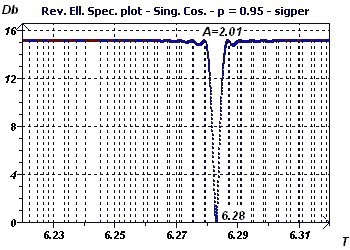
Figure 4-b : Le spectre elliptique inverse (RES) présente un minimum à 6,28 pour un intervalle de confiance de 95%. En bleu la zone de
validité du test de l'ellipse, limites de confiance de la période.
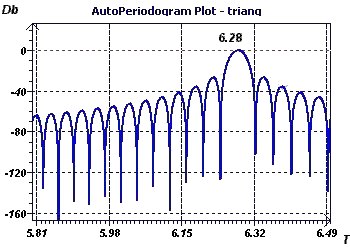
Figure 4-c : Le périodogramme selon Jenkins et Watts, permet de trouver la période de 6,28. Cette méthode est complétement différente de la
régression (On calcule la transformée de Fourier de la fonction d'autocorrélation)
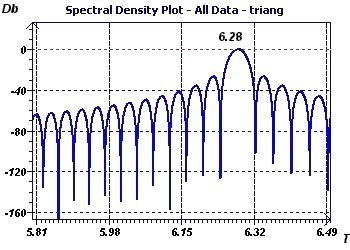
Figure 4-d : L'analyse spectrale selon Blochner adaptée au phénomènes stationnaires conduit au même résultat.
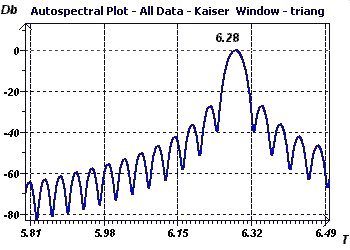
Figure 4-e : L'analyse autospectrale selon Jenkins et Watts constitue l'analyse spectrale classique, (ici avec une fenêtre de Kaiser)
On retrouve la période de 6,28.
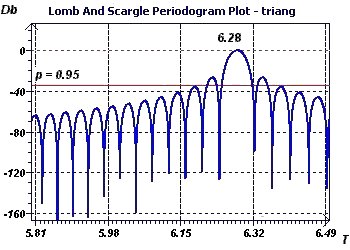
Figure 4-f : Le périodogramme de Scargle confirme les résultats précédents.
Figure 4-g : Le périodogramme de Fisher va tester la fondamentale à 6,27.
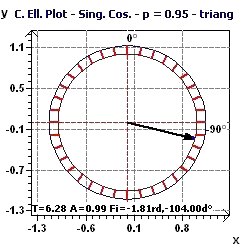
Figure 4-h : Ellipse de confiance : La surface de l'ellipse est petite ce qui traduit une détermination précise de la période.
5 - Signal périodique: sin(t) + sin(3t) + sin(5t)/5 + sin(3t)/3² + sin(5t)/5² avec une période de 2Pi
On va comparer ici le spectre elliptique inverse avec les transformées de Fourier rapides (FFT)
Figure 5-a : La période détectée est 2Pi (6,28). Représentaion du modèle et des points expérimentaux.
Figure 5-b : Le spectre elliptique inverse (RES) permet de trouver la période exacte avec un intervalle de confiance de la période.
Figure 5-c : Transformées de Fourier rapides. Spectre de raies avec une fondamentale à 6,28 (2Pi)
Figure 5-d : Le périodogramme de Scargle trouve la période exacte de 2Pi (voir le pic le plus haut)
6 - Etude de la temperature et l'alcoolisation (Source: Danel, CHRU Lille, France)
Dans cette étude, nous allons observer les périodes correspondantes au rythmes de températures de données provenant de sujets volontairement
alcoolisés et de sujets témoins. La prochaine étape consiste à la construction du modèle.
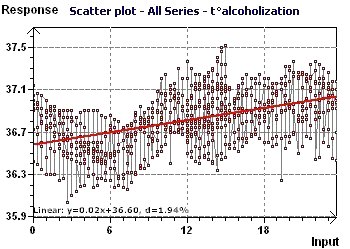
Figure 6-a : La tendance linéaire croit lentement et met en évidence une augmentation de la temperature corporelle.
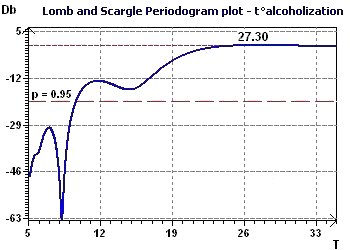
Figure 6-b : Le périodogramme de Scargle met en évidence un pic maximum autour de 27 heures.
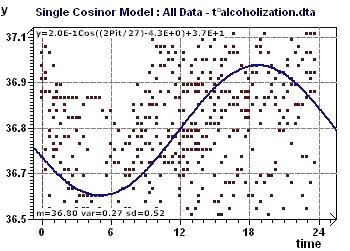
Figure 6-c : Le modèle est construit avec la valeur de la période trouvée. Les données n'ont pas été "détrendées".
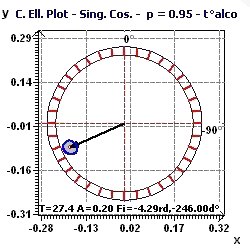
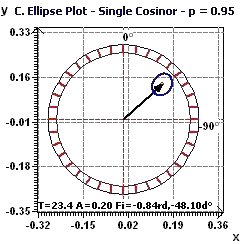
Figure 6-d : Ellipse de confiance (Nelson, Bingham) pour la période de 27 heures. L'acrophase est proche de 18H40 (6:40 PM)
Figure 6-e : Single Cosinor et tests associés pour une période de 27,3 heures.
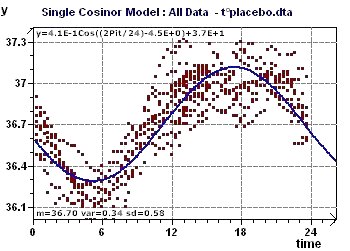
Figure 6-f : La tendance linéaire augmente, ainsi la température du corps augmente au cours du temps
(Une période principale a été trouvée par analyse spectrale)
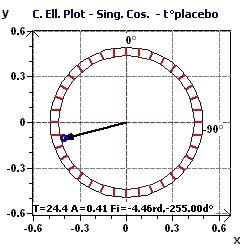
Figure 6-g : Ellipse de confiance pour la période de 24,4 heures. L'acrophase est proche de 17H20 (5:20 PM)
Figure 6-h : Single Cosinor et tests associés pour une période de 24,5 heures.
7 - Etude du Cortisol plasmatique (Source: Brun, Hospices Civils de Lyon, Laboratoire de Radioanalyses, RadioPharmacie, France)
Dans cette étude on va essayer de déterminer la période principale du Cortisol.
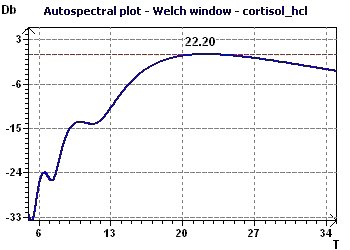
Figure 7-a : Le spectre autospectral selon Jenkins et Watts met en évidence une période principale proche de 22 heures.
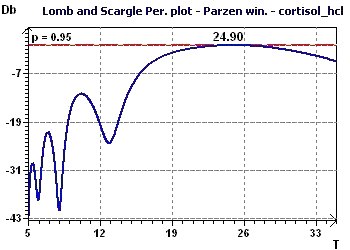
Figure 7-b : Le périodogramme de Scargle met en évidence une période de 24,9 heures.
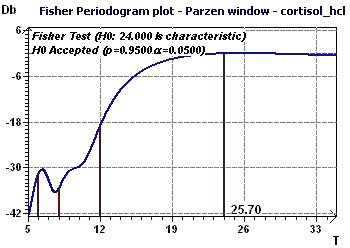
Figure 7-c : Le périodogramme de Fisher met en évidence une période fondamentale proche de 24 heures.
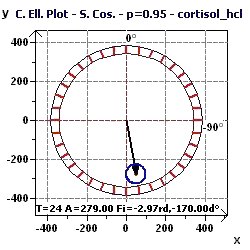
Figure 7-d : Ellipse de confiance du Single Cosinor pour une période de 24 heures.
8 - Etude de la Mélatonine plasmatique (Source: Brun, Hospices Civils de Lyon, Laboratoire de Radioanalyses, RadioPharmacie, France)
Dans cette étude on recherchera les périodes de la Mélatonine plasmatique dans un échantillon de données. C'est difficile de considérer
significatives les périodes supérieures à 24 heures. Ceci peut être partiellement expliqué par la variabilité et la spécificité de
l'échantillonage pour un groupe de sujets dans des conditions données. Le pic de Mélatonine palsmatique usuellement admis est proche de
27 heures ou 3 heures.
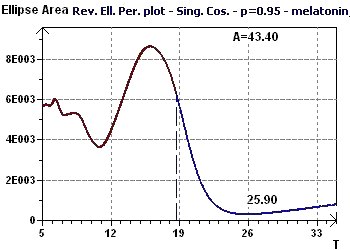
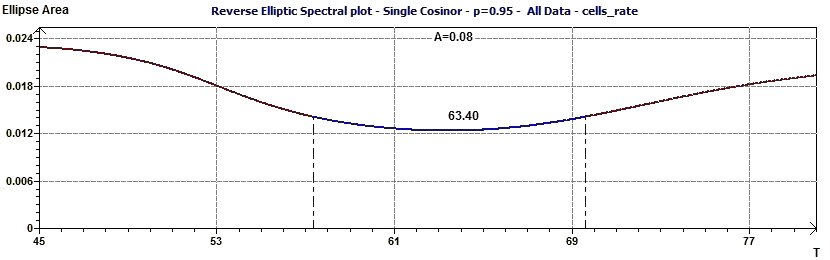
Figure 8-a : Le spectre elliptique inverse (RES) permet de déterminer le pic principal de la période proche de 25,9 heures (p = 0,95,
means confidence interval 95%, α = 1-p)
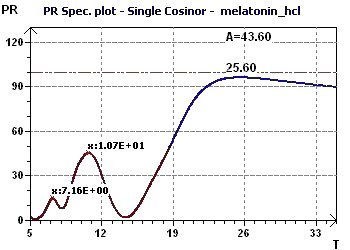
Figure 8-b : Spectre du "Percent Rhythm" détermine une période principale à
25,6 heures. Un pic secondaire à 10,8 heures.
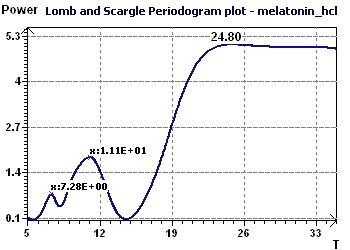
Figure 8-c : Le périodogramme de Scargle détermine une période
principale à 24,8 heures. Un pic secondaire à 11 heures.
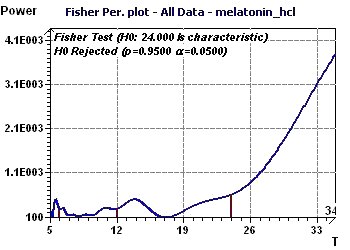
Figure 8-d : Le périodogramme de Fisher determine une période fondamentale de
24 heures et une première harmonique de 12 heures (H0 rejetée signifie que la période fondamentale de 24 heures n'est pas
confirmée)
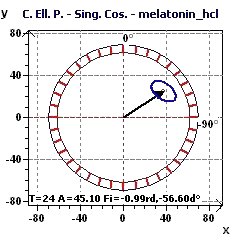
Figure 8-e : Ellipse de Confiance (p = 0,95, a = 1-p) selon Halberg (Période de 24 heures)
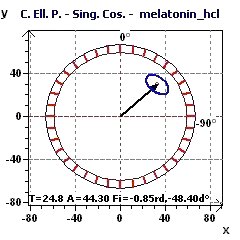
Figure 8-f : Ellipse de Confiance (p = 0,95, a = 1-p) selon Halberg et al. (Période de 24,8 heures)
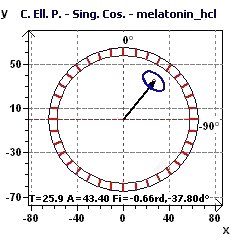
Figure 8-g : Ellipse de Confiance (p = 0,95, a = 1-p) selon Halberg et al. (Période de 25,9 heures)
22 - Exemple la périodicité de la vitesse de prolifération de fibroblastes modifiés (Source: Deschatrette, INSERM U347, France)
Dans cette étude nous allons essayer de mettre en évidence la période de la vitesse de prolifération de fibroblastes transformés.
Figure 22-a : La périodicité principale est mis en évidence par le spectre elliptique inverse (RES). Un exemple appliqué nous montre ici
la vitesse de prolifération, en culture, de fibroblastes humains dont la vie a été prolongée par l'action du gène T-SV40 (L'intervalle de confiance:
Lines pointillées verticales, p = 0.95, means confidence interval 95%, α = 1-p)
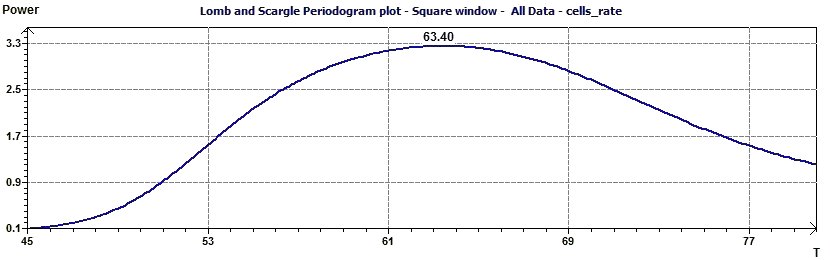
Figure 22-b : La même périodicité est montrée par le périodogramme de Scargle.
23 - Action du méthotrexate sur la résistance cellulaire, longueur des télomères (Source: Deschatrette, INSERM U347, France)
Une modification de la structure de l’extrémité des télomères est observée pendant ce phénomène. En particulier le nombre de paires de bases de l’extrémité
des télomères diminue progressivement pendant la phase d’action du méthotrexate en atteignant un minimum où celui-ci n’est plus actif. Cette phase d’usure
dure deux à trois mois puis la réparation environ deux mois. Nous allons déterminer les caractéristiques de ce phénomène périodique où le nombre de
cellules résistantes est fonction de la longueur des télomères (en kilo paires de bases : kbp)
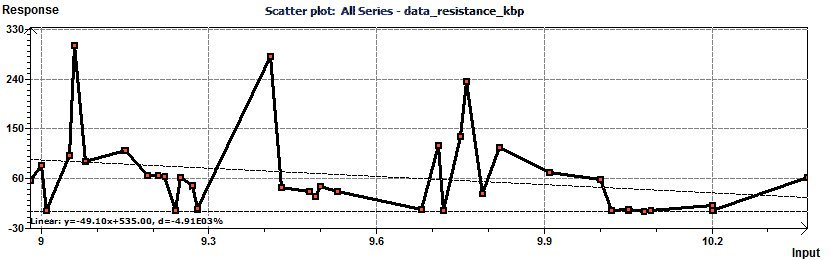
Figure 23-a : L'aspect périodique semble présent.
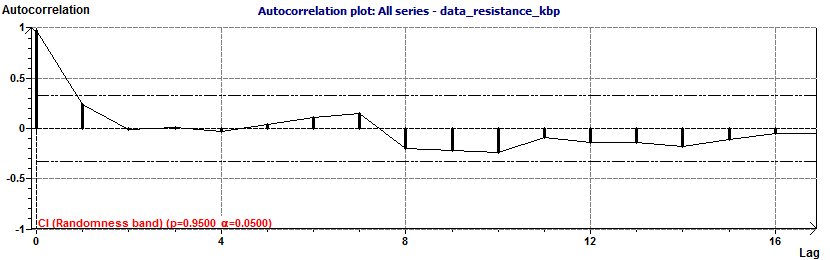
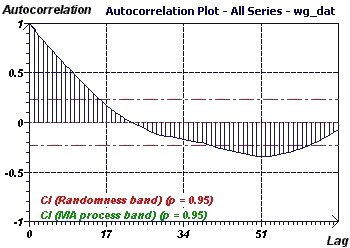
Figure 23-b : Courbe d’autocorrélation : Une partie de la courbe se situe en dehors de la zone correspondant à un phénomène aléatoire,
par contre celle-ci se situe dans une zone pouvant être caractéristique d’un phénomène du type « Moving Average » (p = 0.95, α = 0.05)
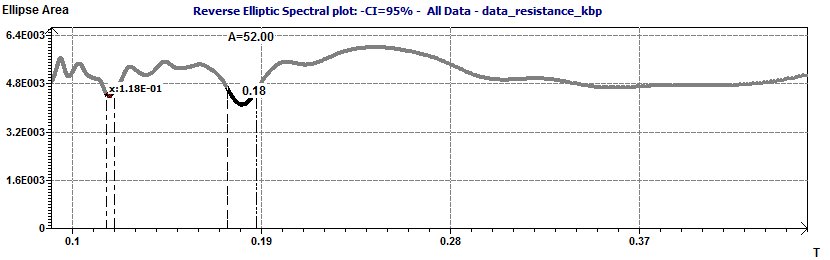
Figure 23-c : Spectre Elliptique Inverse. On considérera la périodes de 0,18 kilo paires de bases.
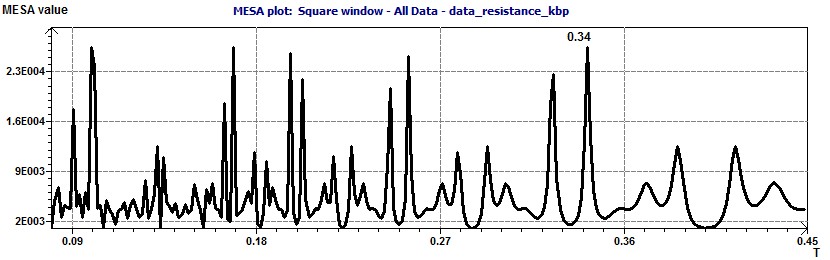
Figure 23-d : Le spectre du MESA (Maximum Entropy Spectral Analysis) montre une période à 0,34 kilo paires de bases.
10 - Etude de la température matinale journalière chez une femme adulte
Les températures ont été relevées depuis le jour 10 (10/07) jusqu'au jour 69 (7/09) On trouve plusieurs périodes
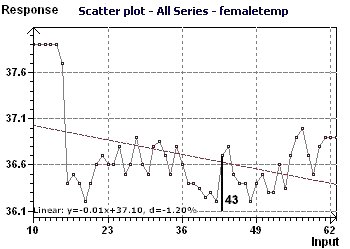
dont une aux environs de 27,6 jours (déterminées par analyses spectrales) Le pic au jour 43 semble correspondre à
l'ovulation. Le scatter plot nous montre que les 4 à 5 premiers points sont des "outliers". Il ne faut
pas les considérer pour calculer les périodes de la température. Ces premiers points ont néanmoins une réalité
physiologique.
Figure 10-a : Le "Scatter plot" révéle l'allure de la courbe de température
avec des "outliers"
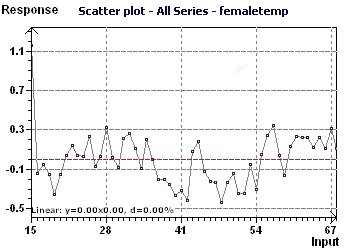
Figure 10-b : Les points aberrants ont été enlevés et on a effectué un "linear detrend".
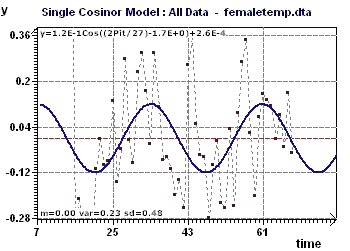
Figure 10-c : Modèle de période 27 jours (Période d'ordre 2) On a soustrait la composante principale du signal total.
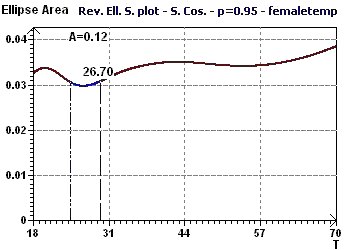
Figure 10-d : Le Spectre Elliptique Inverse permet de mettre en évidence la période
(ordre 2) de 27 jours (après injection des résidus)
11 - Etude du nombre de taches solaires mensuelles de 1900 à 1983 (Source: Andrews et Herzberg 1985)
Cette étude va permettre de rechercher les périodes pour les taches solaires observées à Zurich de 1900 à 1983
(Source: Andrews et Herzberg - 1985) à raison d'une mesure par mois. Les données sont équi-réparties dans le temps ce qui
nous permet d'utiliser n'importe quel type d'analyse spectrale. On va utiliser le "Scatter plot" afin de visualiser
l'aspect général de la répartition des points. L'aspect sinusoïdal semble à priori bien présent. Deux
types d'analyses spectrales de principes totalement différents sont utilisées. On est conduit à la détermination
d'une "fondamentale" de valeur commune. On peut en déduire qu'il y a une périodicité de 123 à 125 mois où l'on peut
observer le même type de phénomène de taches solaires en fréquence.
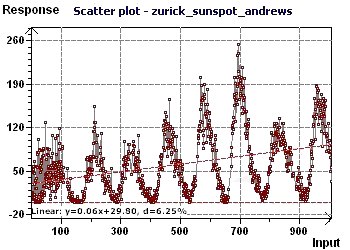
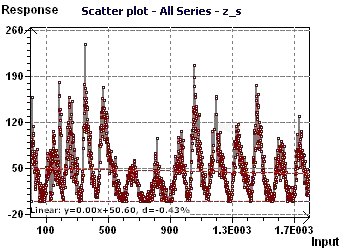
Figure 11-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points. Le caractère
sinusoïdal semble présent.
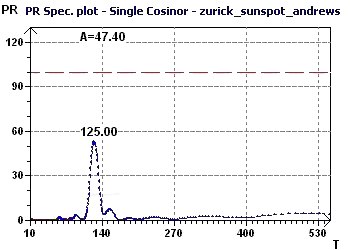
Figure 11-b : Spectre du "percent rhythm", pic de période maximum à 125 mois (soit 10,4 ans)
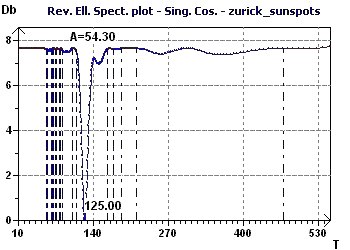
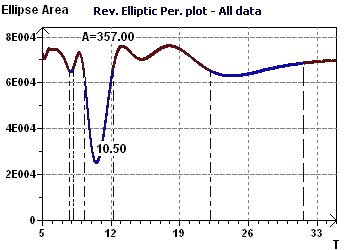
Figure 11-c : Spectre Elliptique Inverse selon Gouthière : Un pic minimum de période à 125 mois (soit 10,4 ans)
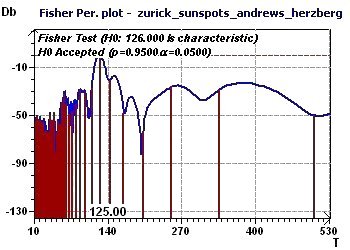
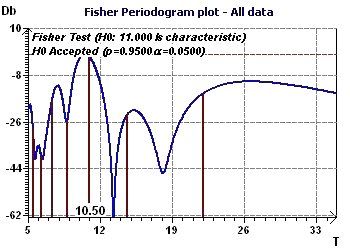
Figure 11-d : Périodogramme de Fisher : une fondamentale à 126 mois (p = 0,95, α = 1-p) (soit 10,5 ans)
12 - Etude du nombre de taches solaires mensuelles de 1749 à 1899 (Source: Andrews et Herzberg 1985)
Cette étude va permettre de rechercher les périodes pour les taches solaires observées à Zurich de 1749 à 1899
(Source: Andrews & Herzberg - 1985) à raison d'une mesure par mois. Les données sont équi-réparties dans le temps ce qui
nous permet d'utiliser n'importe quel type d'analyse spectrale. On va utiliser le "Scatter plot" afin de visualiser
l'aspect général de la répartition des points. L'aspect sinusoïdal semble à priori bien présent. Deux
types d'analyses spectrales de principes totalement différents sont utilisées. On est conduit à la détermination
d'une "fondamentale" de valeur commune. On peut en déduire qu'il y a une périodicité de 133 à 136 mois où l'on peut
observer le même type de phénomène de taches solaires en fréquence.
Figure 12-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points.
Le caractère sinusoïdal semble bien présent.
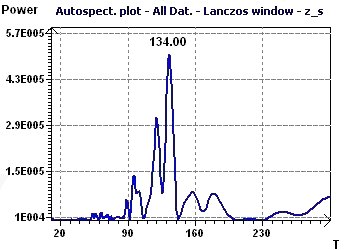
Figure 12-b : Analyse Autospectrale selon Jenkins et Watts : Un pic maximum à 134 mois soit 11,2 années.
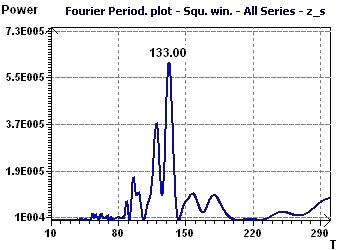
Figure 12-c : Le périodogramme de Fourrier trouve un pic maximum de période à 133 mois (11,1 ans)
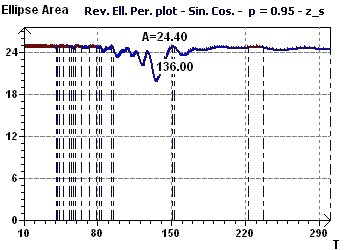
Figure 12-d : Spectre Elliptique Inverse selon Gouthière : Un pic minimum à 136 mois soit 11,3 années.
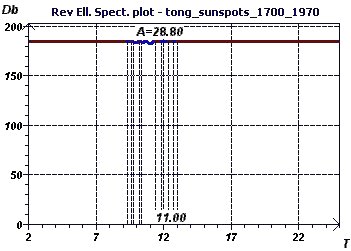
13 - Etude du nombre de taches solaires annuelles de 1700 à 1979 (Source: Tong 1983)
Cette étude va permettre de rechercher les périodes pour les taches solaires observées de 1700 à 1979
(Source: Tong - 1983) à raison d'une mesure par an. Les données sont équi-réparties dans le temps ce qui
nous permet d'utiliser n'importe quel type d'analyse spectrale. On va utiliser le "Scatter plot" afin de visualiser
l'aspect général de la répartition des points. L'aspect sinusoïdal semble à priori bien présent. Deux
types d'analyses spectrales de principes totalement différents sont utilisées. On est conduit à la détermination
d'une "fondamentale" de valeur commune. On peut en déduire qu'il y a une périodicité de 10 à 10,8 années soit 120 à 130 mois où l'on peut
observer le même type de phénomène de taches solaires en fréquence. Ces résultats confirment les résultats précédents
obtenus dans les exemples 10 et 11 (ce qui est remarquable de deux sources différentes)
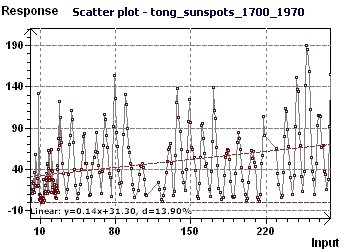
Figure 13-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points. Le caractère
sinusoïdal semble bien présent.
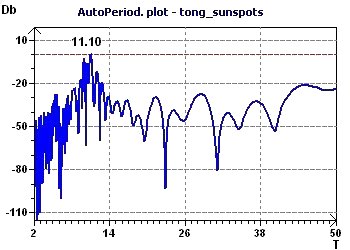
Figure 13-b : Autopériodogramme selon Jenkins et Watts : Un pic maximum à 11 années soit 132 mois.
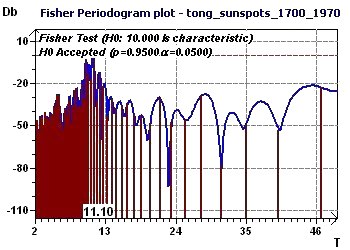
Figure 13-c : Périodogramme de Fisher : Une fondamentale à 10 annés soit 120 mois.
Figure 13-d : Spectre Elliptique Inverse selon Gouthière et al. : Un pic minimum à 11 année soit 132 mois.
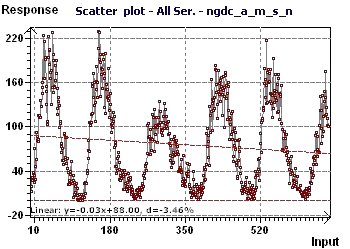
14 - Etude du nombre de taches solaires mensuelles "Américaines" de 1945 à 2000 (Source: National Geophysical Data Center, US Department of Commerce)
Cette étude confirme les études précédentes. On trouve une période proche de 11 années correspondant à un cycle d'activité
solaire. Cette période est conforme à ce qui est communément admis pour la période des taches solaires (Voir Fourier
Analysis of Time Series - Peter Bloomfield p 77)
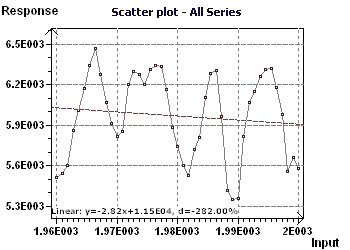
Figure 14-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points. Le caractère
sinusoïdal périodique est présent, la tendance linéire est décroissante.
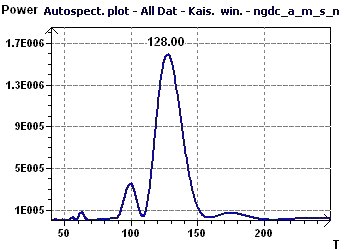
Figure 14-b : Analyse Autospectrale selon Jenkins et Watts : un pic maximal à 128/12 (10,7) soit prêt de 11 ans.
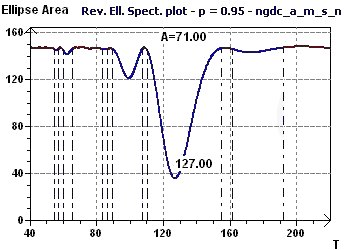
Figure 14-c : Spectre Elliptique Inverse selon Gouthière : une "fondamentale" à 127/12 (10,6) soit prêt de 11 ans.
On peut remarquer qu'il existe d'autres pics de périodes.
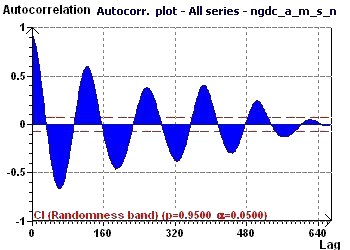
Figure 14-d : Le graphique d'autocorrélation est un bon outil pour mettre en évidence la périodicité. Ce caractère
se manifeste par une courbe sinusoïdale d'amplitude décroissante.
15 - Etude du rayonnement cosmique annuel de 1958 à 2002 à Kiel, Allemagne (Source: National Geophysical Data Center, US Department of Commerce)
Nous avons démontré précédemment (Exemples 11 à 14) au cours de l'étude du nombre des taches solaires qu'un cycle
d'activité solaire d'une période comprise entre 10 et 12 ans était probable. Au cours de cet exemple nous allons
vérifier que cette période est confirmée à travers la mesure du rayonnement cosmique, mesuré ici à Kiel, qui est
une composante de l'activité solaire. On verra que l'on retrouve cette période de l'ordre de 10,5 à 11 années.
Figure 15-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points. Le
caractère sinusoïdal est vraisemblablement présent. La tendance linéaire est décroissante.
Figure 15-b : Cosmic rays : Periodogram of Fisher makes it possible to highlight a fundamental ray of 11 years (p = 0.95, α = 1-p)
Figure 15-c : Le périodogramme de Fisher permet de mettre en évidence une fondamentale à 11 ans (p = 0,95, α = 1-p)
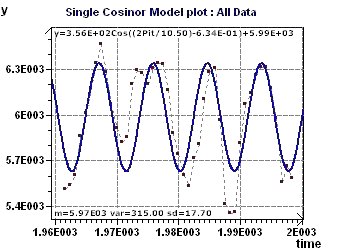
Figure 15-d : Modèle cosinusoïdal (y =356Cos((2Pit/10.5)-0.6)+5990) du rayonnement cosmique de
période 10,5 ans.
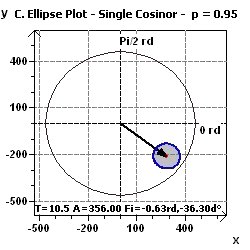
Figure 15-e : Ellipse de confiance (Phase = -0,63 rd, Amplitude = 356) suivant le "Single Cosinor" selon
une représentation anti-horaire en unités internationales.
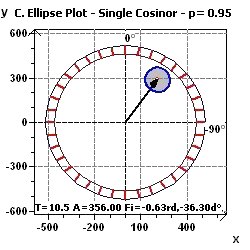
Figure 15-f : Ellipse de confiance (Phase = -0,63 rd, -36,3 degrés, Amplitude = 356) suivant le "Single Cosinor" selon
Halberg et al.
16 - Vélocité de la monnaie, économie des USA 1869-1937 (Source: Friedman et Schwartz)
Dans cet exemple, nous avons recherché les périodicités de la vélocité de la monnaie, puis tracé le modèle prédictif. En pratique un modèle de type ARIMA(n, m)
serait mieux adapté du fait de la forte dépendance des données comme le montrerait un Lag plot, l'identification de n et m se ferait grâce
à la courbe d'autocorrélation et la courbe de PACF.
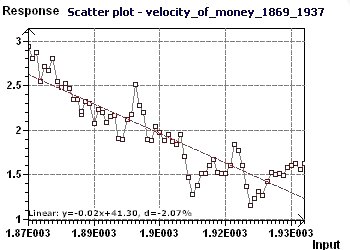
Figure 16-a : Le Scatter plot nous permet de visualiser l'aspect général de la répartition des points.
Le caractère sinusoïdal semble cependant présent comme non allons le voir plus loin.
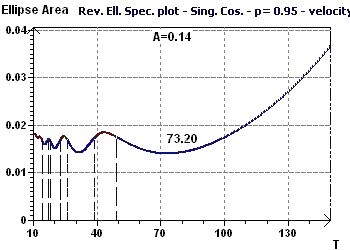
Figure 16-b : Le spectre elliptique inverse permet de déterminer plusieurs périodicités dont une très marquée
à 73,2 années (Les donneée ont subit un "linear detrend" afin de supprimer la tendance et de garder uniquement la composante périodique)
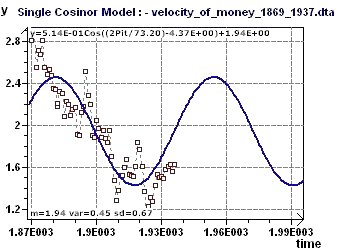
Figure 16-c : Modèle prédictif de la vélocité de la monnaie (période de 73,2 années) jusqu'au environs de
2000 (On poura noter qu'il existe d'autres périodes possibles de valeurs inférieures)
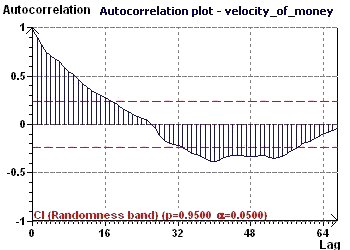
Figure 16-d : La courbe d'autocorrélation nous permet de vérifier que la distribution des données n'est pas
aléatoire. Les donnée sont fortement corrélées.
17 - Variations du prix du cuivre aux USA de 1800 à 1997 (Source: Makridakis, Wheelwright and Hyndman, 1998)
Après détermination de la période, nous construisons le modèle de 1800 à 1997 puis un modèle prédictif qui nous
donnera par exemples les valeurs des variations pour 2000, 2010, etc.
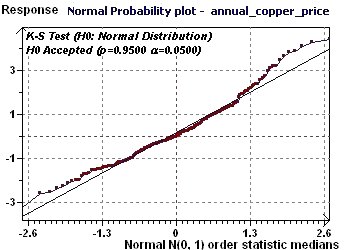
Figure 17-a : La distribution des données est Normale semble-t-il stochastique.
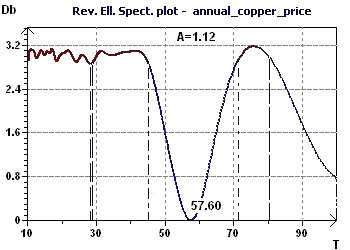
Figure 17-b : Le Spectre Elliptique Inverse (SEI) met en évidence plusieurs périodes dont une plus
marquée à 58 ans.
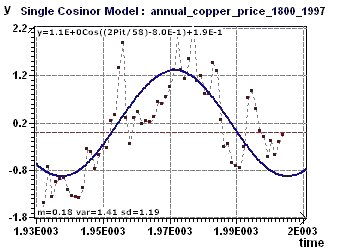
Figure 17-c : Le modèle sinusoïdal est construit sur tous les points de 1800 à 1997 (la période
choisie est 57,7 ans)
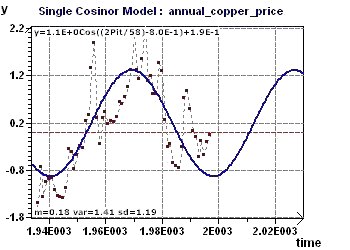
Figure 17-d : Le modèle sinusoïdal est construit jusqu'à 2100 où les valeurs prédites des variations
prévues pour 2000, 2010, 2020 et 2040 sont calculées.
19 - Température, entrainement physique et travail posté de nuit (Source: Mauvieux, CRAPS/STAPS/INSERM Université de Caen, PSA 2003)
Dans l'exemple suivant on a étudié les températures provenant de deux échantillons de la même population. Le premier est
un échantillon de sujets sédentaires travaillant de nuit, le second est un échantillon des mêmes sujets ayant subi
une entraînement physique de quelques semaines. On a constaté que l'entraînement physique a sensiblement provoqué la
modification des courbes de températures en amplitude et en phase (l'amplitude devient plus marquée, la phase diminue)
Une étude des variations de l'amplitude et de la phase a permis de constater que l'amplitude reste constante et que la
phase semble être une fonction du temps.
Figure 19-a : Température chez un groupe de techniciens avant entraînement : Ellipse de confiance selon Halberg et al. avec les
valeurs des paramètres chronobiologiques associés (p = 0,95, α = 0.05)
Figure 19-b : Température chez un groupe de techniciens après entraînement : Ellipse de confiance selon Halberg et al. L'amplitude a
augmentée, la phase a diminuée (p = 0,95, α = 1-p)
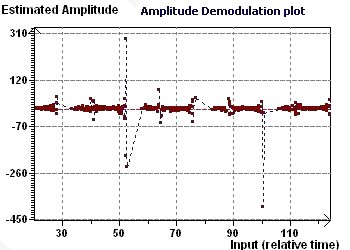
Figure 19-c : Température chez un groupe de techniciens après entraînement : Etude des variations d'amplitude avec le spectre de
démodulation complexe en amplitude. Les variations semblent constantes : l'amplitude n'est pas une fonction du temps.
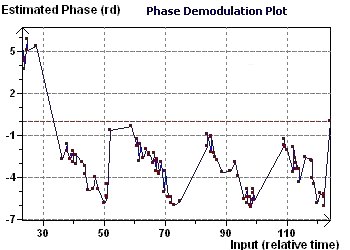
Figure 19-d : Température chez un groupe de techniciens après entraînement : Etude des variations de phase avec le spectre de
démodulation complexe en phase. Les variations semblent ne pas être constantes : la phase est une fonction complexe du
temps voir même périodique.
20 - Salaires annuels aux USA de 1900 à 1970 (Source: Hipel et McLeod 1994)
Dans cette exemple de séries temporelles on va illuster la forte autocorrélation des données. Dans un deuxième
temps on va essayer d'identifier quel type de modèle serait adapté.
Figure 20-a : Le graphique d'autocorrélation montre une forte autocorrélation. On peut suspecter la
présence d'un phénomène de type Autorégressif (AR process) dont on pourra trouver l'ordre à l'aide du graphique du PACF.
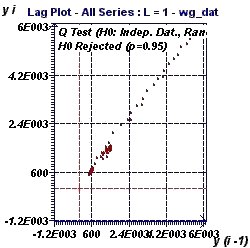
Figure 20-b : Le "Lag plot" ou graphique de décalage décrit une forme linéaire ce qui exclu une
distribution aléatoire des données. Un test de Ljung Box (Q test) permet de vérifer l'hypothèse de non indépendance
des données. La stucture linéaire est caractéristique d'un "AR process".
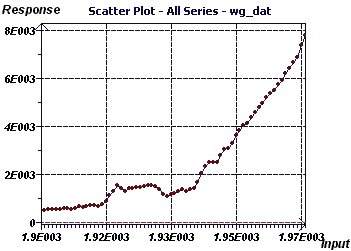
Figure 20-c : Le "Scatter plot" permet de visualiser l'évolution semble-t-il exponentielle des
salaires. On n'observe pas de variation d'échelle ni d'"Outliers".
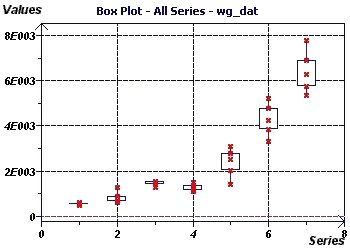
Figure 20-d : De même le "Box plot" visualise cette évolution exponentielle et montre la variabilité
croissante inter-quartiles toute les décennies. On n'observe pas d'"Outliers".
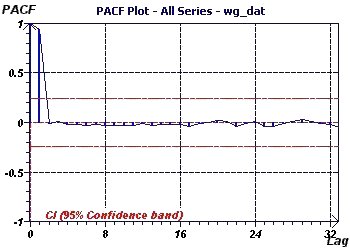
Figure 20-e : Le graphique du PACF ("Partial autocorrelation") montre une valeur significative pour 1.
On peut supposer qu'un "Autoregressive process" d'ordre 1 ou AR(1) serait un modèle bien adapté.
Figure 20-f : L'analyse spectrale selon Blochner nous montre un pic unique très prêt de la fréquence 0 ce qui
confirme que le choix d'un "AR process" semble le mieux approprié.
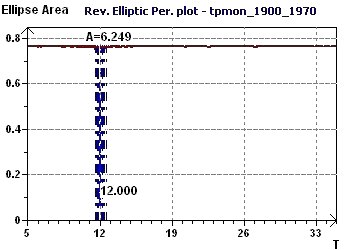
21 - Températures mensuelles en Grande-Bretagne de 1900 à 1970 (Source: Hipel et McLeod 1994)
Cet exemple permet de mettre en évidence une période inconstestable à 12 mois (circannuel) avec différentes méthodes.
Toutes les méthodes donnent unanimement cette valeur de période. Un Single Cosinor permet de donner les paramètres
caractéristiques de ce phénomène rythmique. Nous en déduisons la courbe de prévision des témpératures pour l'année 2005.
(Dans cet exemple les données ont été préalablement traitées pour supprimer la tendance linéaire
qui présente une pente faible, il reste donc principalement après "linear detrend" la composante périodique)
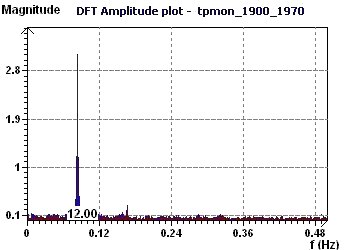
Figure 21-a : Les Transformées de Fourier, comme le périodogramme de Fisher confirme une fondamentale
à 12 mois.
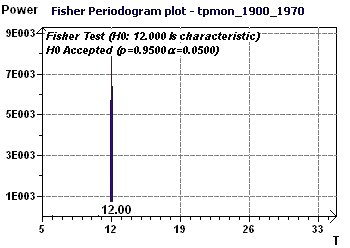
Figure 21-b : Périodogramme de Fisher. La période de 12 mois est caractéristique de l'existence d'un phénomène rythmique (p = 0,95, α = 1-p)
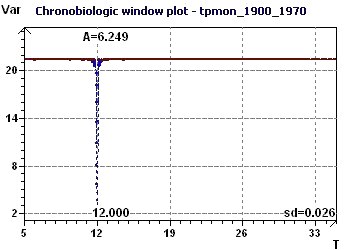
Figure 21-c : La "Chronobiologic Window" de Halberg met en évidence la période de 12 mois.
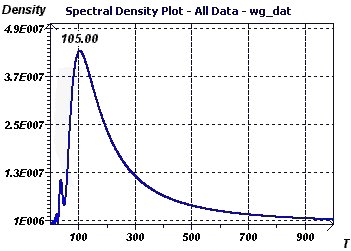
Figure 21-d : De même le Spectre Elliptique Inverse (SEI) retrouve cette unique période de
12 mois.
Figure 21-e : Les tests du Single Cosinor permettent de caractériser ce phénomène rythmique de période de 12 mois (Extrait)
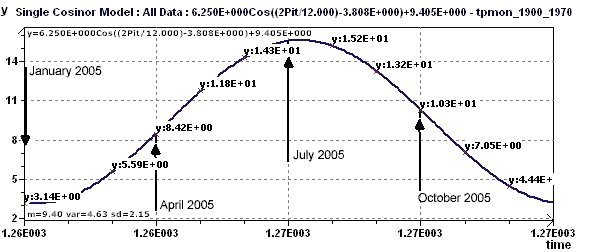
Figure 21-f : Courbe de prévision théorique des températures moyennes en Grande-Bretagne pour 2005 (Janvier 2005 est le 1261ème mois à partir de Janvier 1900)