Chronobiology : Principles and Methods - Pietro Cugini - Medical Semeiology and Methodology
Annali Istituto Superiore di Sanità, 29, 483-500, 1993.
A discipline can be called 'scientific' if dealing with a
field of natural phenomena that are objective and measurable,
possibly not causal but systematic. Chronobiology fulfills these
requirements as it explores biological rhythms which are an
integral part of the organization of living matter. As a matter
of fact, the speculative objective of chronobiological
investigation is the rhythmic repetitivity of biological events
along both phylogenetic (paleochronobiology) and ontogenetic (neochronobiology)
lines.
Chronobiology can be defined as 'the scientific discipline
that quantifies and explores the mechanisms of biological time
structure and their relationship to the rhythmic manifestations
in living matter'.
It must be noted that since biological rhythms are genetically
transmitted, these phenomena necessarily have an inherited
character. This implies that the periodic time is a counivocous
parameter of living functions, which cannot be neglected, as it
is in much of the traditional biomedical thought. Scientists are
aware of the fact that living species live and act in time. The
concept, therefore, of cyclic biological time is not completely
extraneous to scientific doctrine. Traditional biology, however,
considers time as an implicit quantity, relegating it a role of
implicit factor.
Understanding the message of chronobiology requires
renunciation of the concept of 'homeostasis', as well as a
reformulation of the biological principles dictated by C. Bernard.
Chronobiology holds that the physiology of vital functions does
not answer to the laws of steady state, invariance, or the
unconditional return to the initial equilibrium following a
perturbation. Conversely, the rhythmic recurrence of biological
processes substantiates the idea that living matter is subjected
to a continuous variation in state. Accordingly, biological
rhythms represent a syntropic-entropic process with accumulation
and dissipation of vital energies. In bioperiodic machineries
living matter finds the time necessary for the consumption and
the reconstruction of organic materials.
CLASSIFICATION OF BIOLOGICAL RHYTHMS
Biological rhythms can be classified according to numerous criteria.
1. Physical classification
This classification is based on the length of the period of
oscillation. Table 1 details this repartition.
TABLE 1 - Temporal classification of biological rhythms
--------------------------------------------------------
Domain..... ..............Period (Tau)
--------------------------------------------------------
Ultradian.................<20 h
Circadian:...............24 +/- 4 h
dian.................24 +/- 2 h
Infradian:................>28 h
circaseptan...........7 +/- 3 d
circadiseptan........14 +/- 3 d
circavigintan........21 +/- 3 d
circatrigintan.......30 +/- 5 d
circannual..........1 y +/- 2 m
-------------------------------------------------------
h = hours; d = days; m = months; y = year.
The rhythms whose period of oscillation is 24 +/- 4 hours are
defined as 'circadian' (from circa dies, i.e., approximately one
day). The cyclic events with a period of less than 20 hours or
more than 28 hours are defined respectively as 'ultradian' and 'infradian'.
2. Functional classification
Besides the physical classification there exists a subdivision
based on functional concepts that recognizes four varieties of
biological rhythms, i.e., alpha, beta, gamma and delta.
The alpha rhythms coincide with the spontaneous oscillation of
biological functions. Alpha rhythms are subdivided into alpha(s)
and alpha(f) according to whether they are produced in conditions
of 'synchronization' or 'free-running' (see below). The beta
rhythms correspond to the periodicity of the response of
biological functions toward stimulations or inhibitions applied
at different times. The beta rhythms as well exist in the
varieties beta(s) and beta(f) in relation to the presence of
either synchronization or free-running conditions. These two
varieties are further subdivided into beta(s1) or beta(f1) if the
perturbance is physiological, and alpha(s2) or beta(f2) if the
perturbance is not due to a physiological event. Gamma rhythms
regard the periodic oscillation of biological functions being
modulated, perturbed, or influenced by deterministic factors,
either physiological, i.e., gamma(s1) or gamma(f1), or non-physiological,
i.e., gamma(s2) or gamma(f2). Here again, the differentiation
into gamma(s) and gamma(f) varieties depends on the presence of
either synchronization or free-running conditions. Lastly, delta
rhythms, which are also subdivided into (s) and (f) varieties,
correspond to the modification in the periodic oscillation of a
given biological function secondary to manipulation of an alpha,
beta, or gamma rhythm.
3. Mathematical classification
The examination of rhythmic phenomena in organic matter
reveals that there exist events which repeat themselves after a
certain lapse of time as isolated occurrences. These are the 'qualitative,
punctual, discrete, or episodic rhythms' expressed by a binary
condition, i.e., present/absent, event/non-event. For example the
menstrual cycle.
Qualitative rhythms are mathematically describable in terms of
finite quantities (0 or 1) and counted as numerical frequencies.
Therefore, qualitative rhythms could also be called 'frequential
rhythms'.
In living organisms it can be noted that several phenomena
repeat themselves as events which vary in a 'continuum'. In other
words, the phenomenon is always present and measurable, even
though changing as a function of time. Its magnitude reaches the
same level following a given period of time. Therefore, the
period of these phenomena is given by the space of time (duration)
in which the curve reaches the identical level after a complete
oscillation. These periodic events are thus a quantitative
expression if their variability and can be identified as 'analogic
or continuous or quantitative rhythms'. These rhythms are
mathematically expressed by numerical values of a potentially
infinite order.
From a classification point of view, there exists a third type
of biological rhythm consisting in isolated peaks inscribed on
the curve of a quantitative oscillation. Whether these spurts
show a cadence in time, they can be defined 'episodic rhythms'.
4. Descriptive classification
This classification is used mainly for the description of
episodic rhythms or when it is necessary to describe a continuous
periodic event in relation to its peak. The rhythms included
under this heading are diurnal, nocturnal, serotine, vesperal,
morning, daily, weekly, monthly, seasonal, yearly, etc.
Note, however. that these terms define the periodicity only
descriptively and do not lend to any inference on the effective
duration of the period of the recurring phenomenon. Therefore, a
diurnal rhythm is not implicitly circadian; it could be ultradian.
5. Evolutive classification
Biological rhythms, like all biological phenomena, undergo an
evolutive process that tends to modify the periodic properties in
function of chronological age. As shown in figure 1, every
periodic function is defined by its mean level, extent of
oscillation, and timing of oscillatory crest, these parameters
being called respectively, Mesor (M), Amplitude (A) and Acrophase (phi).

Utilizing Clinospectror analysis (see below), both positive
and negative trends (clinous) have been identified for mesor and
amplitude as an effect of age (Fig.2).
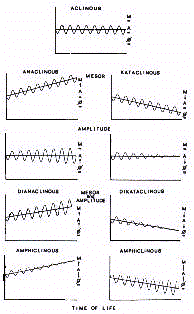
Therefore there are 'dianaclinous' or 'dikataclinous' rhythms
if both properties have a positive or negative trend during the
course of life. Rhythms can also be defined as 'mesor-anaclinous'
or 'mesor-kataclinous', and 'amplitude-anaclinous' or 'amplitude-kataclinous',
if the evolution through chronological time involves only one of
the parameters in either a positive or negative sense. There is
also the possibility of a trend opposite to the two rhythmic
properties defined as an 'amphiclinous' rhythm. Finally, there
can be an 'aclinous' rhythm which is a rhythm that shows itself
to be stable even though the age increases.
6. Duration classification
Observing rhythmic biophenomena it can be ascertained that
some of these are 'permanent or long-lasting' while others are 'transitory
or temporary'. The ovarian cycle is a typical 'transient' rhythm
because it disappears with menopause. The rhythm of body
temperature is instead a permanent rhythm that is found even in
the cadaver in the first 24-h following death.
7. Physiological classification
In considering biological rhythms we cannot neglect the
important role they play in the economy of vital functions. In
this regard it must be kept in mind that there are rhythms which
are 'essential' or 'vital', and rhythms which are 'non-essential'.
The essential rhythms are the pulsatile activity of heart,
respiration, and cerebral electrical activity. The suppression of
one of the first two coincides with 'physical death'. The lack of
the electroencephalic rhythm, as is seen in the flat
electroencephalogram, defines so-called 'clinical death'.
It can be derived from the aforesaid that the essential
rhythms represent biological life. Death coincides, with the
abrogation of these fundamental rhythms. From this perspective it
is seen that life and biological rhythmicity are a counivocous
expression.
Non-essential rhythms are those rhythms whose abolition or
desynchronization has no repercussion on vital functions. Their
lack can, however, contribute to the development of a primary
pathology (protochronopathology). The abolition of non-essential
rhythms can be secondary to a given disease (deuterochronopathology).
8. Biological classification
Examined under the profile of their meaning, biological
rhythms may be found in two very important aspects of life, i.e.,
the conservative and reproductive functions.
The rhythms of the conservative sphere are, in turn, mental
and physical. These two categories can be further identified as
intellective, affective, endocrine, cardiovascular, metabolic,
respiratory, digestive, etc. Reproductive rhythms are, on the
other hand, related to sexuality and fertility.
9. Resistance classification
In biology, the rhythmic manifestation of life have different
values with respect to their robustness.
There exist, in fact, 'resistant' or 'stable' rhythms as well
as bioperiodic events that are 'weak' or 'labile'. The resistance
of a rhythm depends on its role and to which system it belongs.
Basically, resistance is inversely proportional to the
susceptibility to be desynchronized following acute perturbations.
The lability of a rhythm is mostly dependent on its
spontaneous or forced passage to a different order of periodicity
(multiplication or demultiplication of frequency). The rhythm of
the heart is said to be labile because it can easily vary in
frequency over the 24-h span. Only rarely the lability of a
rhythm is due to its abrogation. The abolition of a biological
rhythm is an extremely unnatural event which is very improbable
to occur. Therefore, the disappearance of a given rhythm must be
carefully evaluated and it cannot be established without having
verified that the rhythm has just and simply changed its period.
10. Ontogenetic classification
Biological rhythms are part of the genetic patrimony of living
matter. The oscillators are located in each cell, at every level
of the biological organization. The rhythms begin to act at the
birth of the cell. In metazoes the cellular rhythms take part to
a more complex and general rhythmicity whose expression requires
coordination and maturation. Some rhythms of very high organized
activities, thus, take a certain time for their postnatal
ontogeny.
Rhythms in the formative stages are called 'immature' rhythms,
while those already operant at birth are defined as 'mature'
rhythms.
11. Structural classification
Biological rhythms are natural events which recur
spontaneously, their periodic component being endogenous. The
endogeneous contribution to periodicity can manifest itself
freely (free-running rhythms) or it can be conditioned by
environmental factors that act cyclically as synchronizers (synchronized
or masked rhythms). The free-running rhythms, therefore, may be
transformed into synchronized rhythms, and the endpoint of this
interplay is a 'masking effect' exerted by the exogenous
component on the endogenous bioperiodicity. In nature, the overt
manifestation for most biological rhythms is the combination of
the endogenous component plus the exogenous entrainment. In this
case, the masking effect results in a synchronized rhythm, and
the external factors of masking can be defined 'entraining agents'
or 'zeitgebers' or 'synchronizers'.
Importantly, the manipulation of an environmental synchronizer
may cause a disturbance of the endogenous periodicity which
results in a phenomenon of 'external desynchronization'. The
dyschronic effect must be kept in mind when dealing with a
biological rhythm lacking periodicity. This means that the
abrogation of a given periodicity may be attributed to an
exogenous mechanism being not primarily dependent on an intrinsic
defect of internal rhythmicity.
Interestingly, the masking effect may be not only exogenous
but also endogenous. The endogenous masking effect can be used to
explain the complex conditions of rhythm loss not explainable in
terms of cause and effect. For example, the loss of the sleep-waking
rhythm produces an endogenous masking effect on numerous other
rhythms causing their periodicity to be abrogated (see below).
12. Consistency classification
There are rhythms that regard one concrete entity, i.e., 'real
rhythms'. Other rhythms are instead the mere expression of a
computational parameter, i.e., 'virtual rhythms'. The
nychtohemeral profile of cortisol rhythm, when studied in blood,
coincides with the within-day variations of its concentration in
plasma or serum. By contrast, the circadian rhythm of pH is
caused by the interplay of numerous factors each one
characterized by its own rhythm.
13. Constitutive classification
There are biological rhythms which refer to a single variable
(something that is definable by its characteristics), i.e., 'elementary
rhythms', and others which attain to complex functions, i.e., 'composite
rhythms'. Examples may be the circadian rhythm of prolactin, on
one side, and the circadian rhythm of mood, on the other.
If a rhythm is found to be complex, its eventual abolition
could be dependent on an internal desynchronization among the
constituent cyclic factors or mechanisms. Sometimes, the
aperiodicity is merely due to changes in phase resulting in an
antiphasic oscillation of the cycles which contribute to the
complex rhythm.
14. Hierarchical classification
In the magnificent organization of bioperiodic phenomena it
has been found that some rhythms play a prominent role in
conditioning other biological cycles. These rhythms are called 'guide
or primary or independent rhythms' while the driven rhythms are
called 'guided or secondary or dependent rhythms'. Guide rhythms
have a strategic importance in the sense that their presence is
essential for the dependent periodicity. The lack of a guide
rhythm usually produces desynchronizing effects mostly due to the
abrogation of the rhythmic interplay. The interruption of the
relationship between primary and secondary rhythms causes a
phenomenon called 'internal desynchronization'. The guided
rhythms will be absent due to an induced effect. Such a dramatic
repercussion is called 'endogenous masking effect'. The
endogenous masking may help us in understanding and
interpretating the chronopathology of some biological rhythms.
GENESIS OF BIOLOGICAL RHYTHMS
The capacity to undergo rhythmic oscillations is a
characteristic intrinsic to living matter. A fundamental
statement of chronobiology states 'many rhythms persist even in
complete isolation from the major known environmental cycles'.
This affirmation clarifies that the natural rhythms can be
considered to lay outside of the period of the geophysical cycles.
This means that living matter has its own time, i.e., the 'biological
time'.
Assuming time as a fourth dimension of biology, one can
conceptually and syllogistically argue that a Chronome exists
into the Genome. Besides the physical (physemes) and chemical (chememes)
signals, one can assume that the genes provide information also
in the form of 'chronemes', i.e., signals of periodic type. In
such a way the process of clonation is timed by determined
periods, and results in a combination of quantal and temporal
messages which cause the biological functions to quantitatively
change according to a programmed spectrum of periodicities.
Speculatively, one could presume that the temporal signals find
their periodic genesis within the helicoidal spirals of DNA where
the chronome should reside. The DNA double helix could act as a
metronome generating a vibration whose length is the period of
clonation.
It has been suggested that the gene inherits not only the
capacity to clone (Ergon) but also the capacity to endure (Chronon).
The concept of Chronon refers to the expression of genes as a
function of the chronological time which is linear, irreversible
and progressive. The concept of Chronome relates to the
expression of genes according to the chronobiological time which
is cyclical, irreversible but recursive. Accordingly, the
chronological time could be seen as the summation of the iterated
periods which constitute the time base of biological rhythms.
BIOLOGICAL CLOCKS AND CONTROL OF BIOPERIODIC PHENOMENA
Biological periodicities are driven by a genetic program to
run according to a temporal duration (biotemporality) which
causes a recursivity in a spectrum of frequencies ranging from
milliseconds to years.
The temporal effect of genetic programming, the chronome, is
the endogenous component for which the biological rhythms
originate as 'free-running' bioevents. The free-running rhythms
reflect the 'time of the body' which is independent from the
environmental time measured by the clock, the 'physical time'.
The free-running rhythms reflect the endogenous mechanisms of
cyclic temporization whose expression is morphologically seen as
an internal clock, a 'biological clock'.
Observing the animals integrated into their environment, it
can be noted that the endogenous rhythms are usually not 'free-running'.
The 'time of the body' is masked, and the spontaneous biological
rhythms are obliged by the exogenous cycles to adjust their
period in accordance. This means that the biological time has
innately the capacity to uniform itself with the physical time.
Therefore, events that perturbate the environment can modulate
the periodic cadence of the genetically determined endogenous
rhythms. The strongest interferences are those provided by
systematic events having a cyclical character in their
manifestation. The light-dark alternation, meal timing schedule,
social routines, including work shifts, etc. (see below) are
deterministic as entraining agents.
In the entrainment of endogenous rhythms many structural
entities intervene with a role of mediation (Table 2).
TABLE 2 - Central nervous structures involved in the
chronoregulation of biological functions
-------------------------------------------------------------
Suprachiasmatic nuclei
Olfactory bulbs
Fornix
Septum
Limbic structure
Hippocampus
Preoptic area
Retino-hypothalamic connection
Midbrain raphe nuclei
Ventromedial hypothalamus
Dorsomedial hypothalamus
Locus coeruleus
Brain stem
Autonomic nervous system
Superior cervical ganglic
Pineal gland
-------------------------------------------------------------
The most important determinants of biological timing are the
endogenous oscillators, structures of the organism that function
as rhythmic 'pacemakers'. Other machineries of synchronization
are the 'pace-resetters', elements of the organism that regulate
the temporal structure of one or more rhythms in response to one
or more environmental synchronizers. The informative
relationships between pacemakers and pace-resetters are
determined by special connecting structures called 'transducers'
that translate the exogenous stimuli to the internal clocks.
Transducers may have either negative or positive effects on the
oscillators. The series can be integrated by the 'modifiers' and
the 'logic controllers' which act, respectively, in modifying and
controlling the exogenous and endogenous stimuli.
With regard to biological clocks there exists an eternal
diatribe between positivists and negativists. The prevalent
opinion is positivistic in the sense that the biological clocks
are accepted as identifiable entities which reside inside tissues
and organs. Those who believe in the existence of biological
clocks assert that these structures of self-sustaining timing
play a primary role in coordinating the miriad of peripheral
biological rhythms. Such a coordinative capacity presupposes a
leadership with which the biological clocks drive the phase of
the rhythms provided by each cell of the organism. This implies
that the biological clocks are formally equipped to ubiquitarily
interact with all the cells by means of neural, physical and
chemical messages. For this reason they are prominently located
inside the non-mitotic structures of the nervous system, both
encephalic and spinal.
The structural organization of biological clocks is difficult
to be deciphered. An attempt will be made here by presenting the
principal models. The Model I, the simplest, is made by an
oscillator that times a second oscillator, and so forth. This
primordial model proposes a linear cybernetic control. The Model
II describes a primary oscillator followed by a series of
oscillators in succession. The Model III proposes an interaction
between various oscillators of equal hierarchical importance
arranged in a cybernetic network. The control by nodal clocks
explains the occurrence of collateral interactions conditioning
the mechanisms of positive or negative feedback. This interactive
mechanism of chronoregulation has been called 'feed-sideward'.
Chronoanatomic research has brought to light a series of
structures responsible for rhythmic programming and
chronobiological integration of the organism with the environment.
Information on the neuroanatomical structures involved in the
central regulation of biological rhythms derive essentially from
animal studies. Table 3 lists the structures which are presently
recognized to play a rhythmogenic role as oscillators.
TABLE 3 - Central structures involved in the coordination
of oscillating biological functions
-------------------------------------------------------------
Pacemakers
Paceresetters
Modifiers
Transducers
Logic-controllers
Synchronizers
-------------------------------------------------------------
DESYNCHRONIZATION, RESYNCHRONIZATION, CHRONIZATION
Chronobiological studies provided evidence that various
environmental factors act hierarchically as synchronizers of
biological rhythms. The most powerful synchronizer is the light-dark
alternation. Isolated from geophysical temporality, human beings
progressively tend to delay the resting time. This phenomenon
occurs even in conditions of perennial light or darkness. A rapid
change in time zones (passing through three or more time zones),
as occurs in transmeridian flights, gives rise to a
psychophysical disturbance commonly known as 'jet lag syndrome'
prominently due to the dyschronism between biological time and
physical time. The resynchronization following geographical
dyschronism occurs with a phase shift of about 90 minutes every
24-h. It is, however, necessary to keep in mind that the
direction of time zone transiction is crucial. In east-west bound
flights, travellers must recuperate a time span equal to the
temporal difference between the two time zones. In west-east
bound flights, subjects must recuperate 24 hours minus the
difference in time zones, i.e., the physical time already passed
in that zone which was not biologically 'lived' by the travellers.
This implies that the resynchronization takes much more time. The
resynchronization can be, however, accelerated or delayed by
numerous factors (Table 4).
TABLE 4 - Factors affecting resynchronization rate
------------------------------------------------------------
Acceleration..................Retardation
------------------------------------------------------------
Extroversion..................Introversion
Serality......................Manility
Phase advance.................Phase delay
Delay shift...................Advance shift
Labile rhythms................Stabile rhythms
Strong temporal pressures.....Weak temporal pressures
Higher performance task.......Lower temporal task
Younght.......................Ageing
Low neuroticism...............High neuroticism
Low pulse/respiration ratio...High pulse/respiration ratio
------------------------------------------------------------
The meal schedule is also a robust synchronizer. Subjects fed
a complete meal only once a day will show a phase shift for many
biological rhythms toward the hour that the meal is given. Social
routines (sociotemporality) are also important, especially shift
work. A random shift can produce desynchronizing effects for many
periodic functions, especially those related to physical and
mental performance. Other environmental agents causing
dyschronism are stress, fasting, fatigue, etc., if abnormally
prolonged in time and/or cyclically repeated.
Several drugs can induce desynchronization as well. The lists
of these drugs should compose a new chapter of pharmacology to be
used in pharmacological surveillance.
Interestingly, some drugs may be used for resynchronizing the
biological rhythms disturbed by exogenous interferences. These
drugs are called 'chronizing agents or chronizers'. A list of the
pharmacological molecules promoting chronization is reported in
Table 5.
TABLE 5 - Pharmacological agents used as chronobiotic drugs
-----------------------------------------------------------
ACTH
Barbiturates
Tricyclic antidepressants
Lithium
Nomifensine
Xantine derivantes
Levodopa
5-hydroxytryptamine depletors
Indomethacine
Melatonin
-----------------------------------------------------------
ONTORHYTHMOGENESIS AND GERORHYTHMOCLINIA
As an innate expression of vital dynamism, biological rhythms
originate at the time of fecondation, the so called 'ontogenic
zero point'. In order to show an overt expression and integration,
some rhythms require a central coordination which controlled by
biological clocks whose development is related to the maturation
of the central nervous system.
The need of maturation indicates that the ontogenesis of
biological rhythms results from the recruitment, organization and
phase synchronization of the myriad of cycles generated by cells
at the peripheral level.
It is important, however, to remark that some rhythms which
require a high degree of integration can be already found in
fetuses. The fetal synchronization reinforces the idea that
maternal influences of cyclical nature are active on the temporal
organization of bioperiodic functions in utero.
After the period of maturation, what is the destiny of
biological rhythms as a function of chronological age? In other
words, what is the effect of aging on biological rhythms?
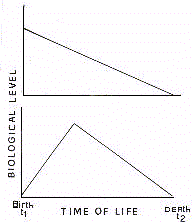
In traditional biology, the aging process is thought to
consist in a phenomenon of linear loss for biological functions (Fig.3).
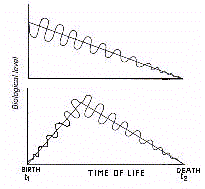
Chronobiology considers aging in the context of cyclicity
which characterizes biological functions. Studies done in this
regard have demonstrated that senescence is associated with a
decline which affects the mean level (gerontologic decline of
tonic activity), and the extent (gerontologic decline of phasic
activity) of oscillation, as well as a shift in the phase (gerontologic
rephasement) and/or a change in the period (gerontologic
demultiplication/multiplication) of biological rhythms.
Accordingly, it can be said that aging is a process associated
with a trend (clinous) which is negative for height and
oscillatory extent of bioperiodic functions. This implies that
the effects of senescence consist in a model of periodic-linear
regression, in which one can see the combined decline of the
oscillation in its mean level and amplitude, i.e., a phenomenon
of gerorhythmoclinia (Fig.4).
Presently, the periodic-linear regression analysis of
gerontological trends of biological rhythms is feasible by means
of the Clinospectror method. This procedure, developed by this
author, combines the estimation of the oscillatory changes,
period by period, as a function of linear advancing age. The
model of the gerontological destiny of biological rhythms is
represented by a curve, i.e., the gerorhythmoclinogram (Fig.2).
Interestingly, the clinorhythmometric study of senescence has
documented that some biological rhythms may show a decline (kataclinous
rhythms or katarhythms), some others may exhibit an amplification
(anaclinous rhythms or anarhythms), in either the mean or
amplitude of oscillation, and, finally, some others may appear
not to change at all (aclinous rhythms or isorhythms), with
advancing age. The gerorhythmoclinograms of these trends have
been already illustrated in figure 2.
The kataclinous trend is a typical expression of rhythms 'causative'
of senescence. The anaclinous trend, by contrast, represents the
periodic-linear model of rhythms 'adaptive' to aging.
DEFINITION OF BIOLOGICAL RHYTHM
In the preceding paragraphs, bioperiodic phenomena have been
treated as temporal signals whose variation may be expressed by
discrete values coincinding with the sampling time.
It must be stressed that a discrete time series is not a
faithful reconstruction of the signal as the approximation
depends on timing and density of collected data (Fig.5).
In the discretization of bioperiodic phenomena there is the
risk of systematic errors, any temporal series being constituted
by an intrinsic component which is superimposed by occasional or
random elements. The discrete series can, therefore, be
contaminated by aberrant values, the so called 'biological noise',
not belonging to the systematic component of the periodic
variation (Fig.6).
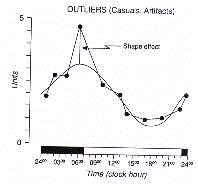
In order to remove the biological noise
due to aberrant values, the so called 'outliers', the periodic
signal has to be geometrically approximated by a curve adjusted
to the raw series of data (Fig.7).
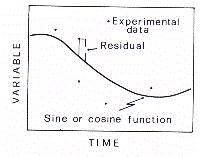
As the signal is periodic, the analytical curve has to be
representative of the harmonic oscillation. Therefore, one can
assume that a biological rhythm is better expressed by the
oscillating wave which optimally fits the discrete signal in its
periodic fluctuation. In line with this thought, one can suggest
that a biological rhythm is by definition 'the periodic component
of a temporal series of biological data whose waveform profile
has been analytically validated'. In other words, a biological
rhythm is 'a biosignal whose period of oscillation has been
validated by analytical models of periodic regression using one
or more harmonic components'. Assuming such a definition, one can
argue that a discrete variation of temporal biodata is not
implicitly a pattern demonstrating a biological rhythm. Obviously,
the analytical resolution of a discrete biosignal doesn't imply
that the biological rhythm is arranged in a perfect sinusoidal
shape. The sinusoidalization is just a model for removing the
aleatory components which causes biological noise and, thus,
biometric disturbance.
Furthermore, there are other valid biostatistical reasons that
recognize the harmonic representation as the ideal signal of
biological cycles. As a variation occurring over the 24-h scale
is not an implicit demonstration that the pattern varies
according to a 24-h period, there is the need to statistically
validate the oscillation in its periodicity. The rhythm detection
level may be statistically verified assuming an 'alpha'
probability (P) of less than 5% for the null-hypothesis of non-oscillation
(zero-amplitude). Using the harmonic model, the biological
rhythmicity may be, thus, statistically validated in its
significance against the probability of P<0.05 that the extent
of oscillation is due to the effect of randomness.
The periodic regression methods used in the analytical
detection and sinusoidal testing of discrete time series of
biodata are discussed in the following chapter.
CHRONOBIOLOGICAL METHODOLOGY OR CHRONOBIOMETRY
In biometrically processing temporal series of biodata, time (T)
may be regarded as a systematic parameter which is independent on
the biological variable under scrutiny. Time illustrates how the
biovariable changes, but it is not the causal determinant of that
change, which, in turn, depends on the dynamic properties of
living matter.
Statistically speaking, phenomenon Y and time T are associated,
but time is not a random variable, its progression being
numerically predictable.
In general, the level of Y (Yt) at a given time (t) is related
to the precedent value. For this reason, any temporal series may
be said to be autoregressive and historical. If the relationship
between Y and T maintains itself unchanged, we will have a linear
temporal phenomenon. If the relationship changes spontaneously we
will have a non-linear temporal event. If the relationship
resumes the same value at t time we will have a cyclic phenomenon.
In descriptive terms, temporal data of a cyclic phenomenon,
based on a given unit of time can be divided into various
components: 1. a fundamental harmonic component that expresses
the true periodic structure of the rhythmic phenomenon; 2. one or
more subharmonic components whose period is a submultiple of the
principal wave; 3. a random component that corresponds to the
noise eliminated by the oscillatory curve.
Thus, biological noise is typical in a discrete series, and it
influences the biometrical estimates of numerical statistics.
However, biological noise is not accounted for in the continuous
series, and it has very little influence on analytical statistics.
In biometrically analyzing time data series, chronobiology
applies both methodologies, i.e., 1. numerical or non-inferential
or macroscopic chronobiometry; 2. analytical or inferential or
microscopic chronobiometry.
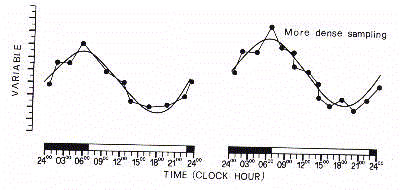
I. NON-INFERENTIAL CHRONOBIOMETRY (MACROSCOPIC ANALYSIS)
Non-inferential chronobiometry is principally based on
measures of central location and dispersion of data sampled at
each time point (Fig.8).

The within-day profile of mean values that results from this
analysis may be called the 'chronogram'. Importantly, in each
point the dispersion around the mean may be measured in terms of
standard deviation (SD), standard error of the mean (SE or SEM),
or 95% confidence limits (95%CL).
The true effect of time on temporal distribution of data may
be ascertained by means of the 'one-way variance analysis' (one-way
ANOVA). The homogeneity of variance in each time point (homoschedasticity)
may be verified by means of Bartlett's test or Duncan's test.
The estimates on the chronograms are as follows: 1. overall
mean level; 2. peak level; 3. peak time (zenith); 4. trough level;
5. trough time (nadir); 6. difference between peak and trough
levels; 7. coefficient of variation for time-qualified mean
levels.
II. INFERENTIAL CHRONOBIOMETRY (MICROSCOPIC ANALYSIS)
The analytical approach to time data series includes various methods.
A. Inferential chronobiometry with unknown period
This type of inferential chronobiometry is based on the
principle that every quantifiable temporal variation (signal) can
be represented by a sinusoidal wave (fundamental harmonic wave).
The analysis is mainly used for two purposes: 1. to find the
period that represents the signal; 2. to recognize a signal by
means of its frequency spectrum.
1. Analysis of the best fitting period (periodogram)
In this type of analysis the best fitting waveform profile is
found using the function
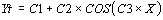
The most important coefficient in this formula is C3 which
corresponds to the period which optimally approximates the raw
data time series.
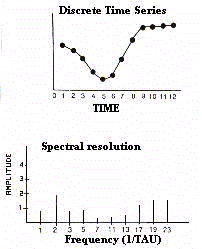
2. Spectral analysis
The analysis of spectral resolution (Fourier analysis) is one
of the most important methods of numeric elaboration of signals
whether they are discrete (digital signals) or continuous (analogic
signals).
A digital signal is a series of values separetely arranged
along a given interval of time to give a sequence of discrete
numbers which are the instantaneous expression of a continuous
function. An analogic signal is a continuous series being a
function of time (t).
The discrete signal for the resolution in a harmonic series (discrete
Fourier Transform) must be represented in terms of X values
equispaced in time. Therefore, the formula is
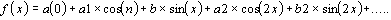
A relationship exists between the sampling numerosity (n) and
time (t)
t = nI
where I is the interval of sampling. Given the equidistance of
values, t will correspond to the time cycle or period (TAU) or
duration of the signal itself.
The continuous signal for the decomposition in harmonic
components (Fourier Transform) has to be known in the formula of
its periodic resolution as the equation has to be included in the
analytical procedure with the coefficients C1, C2, C3 of its
waveform profile.
Spectral analysis consists in the transformation of the
sequential signal, i.e., a temporal entity, into a frequency
spectrum, i.e., a frequential entity. The spectrum of the
resolved frequencies is the microstructure of the decomposed
signal (Fig.9).
Assuming the periode of revolution to be equal to TAU, the
formula for spectral analysis can be rewritten
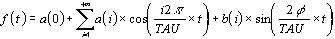
The frequential resolution describes the harmonic components
assuming that every variation of a given duration can be
described by a sinusoidal wave of equal period (fundamental
harmonic) and by even or odd submultiples of these (secondary
harmonics). The harmonics constitute the so called 'formants'
according to which the signal can be analytically reconstructed
as the sum of sine waves (Fig.7).

Therefore, a frequential resolution is a way of recognizing a
signal by its intrinsic structure, as it is probabilistically
impossible that the oscillatory properties of the formants, which
are expressed by the parameters amplitude and phase, might belong
to a different pattern of discrete or continuous values.
Accordingly, the fundamental use of spectral analysis is 'pattern
recognition'.
B. Inferential chronobiometry with known period
Chronobiology, in its incessant methodologic development, has
been oriented mainly towards the methods of periodic regression
analysis in which the period of oscillation is known 'a priori'.
The reasons for this methodological preference depend on the fact
that in biology and medicine it is necessary to know whether or
not biophysical or biochemical functions maintain the
physiological periodicity within the recognized spectrum of
biological rhythmicities (see Table 1). Obviously, in this
validation one must know 'a priori' the period to be validated.
Accordingly, the methods of inferential chronobiometry with a 'prefixed'
period all propose the probabilistic validation of the null
hypothesis of zero-amplitude for that a given period of
oscillation. In this manner, all the methods show the advantage
of estimating the statistical significance of the rhythm under
scrutiny (sinusoidality testing) which is not methodologically
detectable by using the methods cited above.
Importantly, the sinusoidality testing is based on the P level
of statistical probability (rhythm detection level) according to
which the zero-amplitude assumption is rejected. A rhythm is said
to be 'significant' or 'not significant' whether P is
respectively <0.05 or >0.05. The postulate zero amplitude
is checked by computing the 'Percent Rhythm (PR)' which is the
percentage of variability accounted for by the harmonic function
with reference to total variability of experimental data made
equal to 100%.
The methods of inferential analysis with known period give
rise to descriptive, integrative and evolutive chronobiometry or
rhythmometry.
1. Descriptive chronobiometry (descriptive rhythmometry)
Descriptive inferential chronobiometry encompasses various methods.
1.1. Cosinor analysis
In descriptive rhythmometry the most important method of
periodic regression with a fixed period is called 'Cosinor
analysis'. The Cosinor procedure can be separated into two main
methods: Single Cosinor and Population-Mean Cosinor. Both methods
are based on a sinusoidal approximation using a cosine function.
However, Single Cosinor deals with the analysis of a single time
series regarding a single subject or a group of individuals. The
Population-Mean Cosinor elaborates by summarization the
rhythmometric data obtained by Single Cosinor from several
individuals of a given group.
Cosinor analysis applies as a trigonometric operand the cosine
because zero degrees correspond to the reference time or zero
time of the rhythm. Zero time coincides with midnight for
circadian rhythms, winter solstice (22 December in the northern
hemisphere, 21 June in the southern hemisphere) for circannual
rhythms.
Cosinor analysis approximates the following equation to
experimental data using the least squares method for minimization
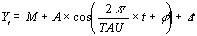
where, M is the mesor (acronym for Midline Estimating
Statistic of Rhythm), the mean level of oscillation, A is the
amplitude, the extent of oscillation from the mesor or half of
the total oscillation, Pi is 3.14159265, TAU is the chosen period,
t is a temporal fraction of the cycle, an instant of the whole
revolution, and phi is the acrophase, timing of the crest of
waveform profile (W).
Therefore, Cosinor analysis quantifies the best fitting
sinusoidal wave in four parameters: M, A, phi and W that
represent the properties of the rhythm for that ultradian,
circadian or infradian period.
Cosinor analysis quantifies further parameters such as the 'percent
rhythm, (PR)' and the 'rhythm detection level (P)'. The waveform
profile can be, thus, validated whether or not it rejects the
null hypothesis of zero-amplitude at a statistically significant
level of probability. This means that the rhythm is validated as
statistically significant for that a given period of oscillation
tested by Cosinor.
In the cosine formula, phi is expressed in negative
sexagesimal degrees in order to represent the parameters
amplitude and acrophase on a polar diagram by means of a single
vector turning in a clockwise fashion (see below).
Cosinor method expresses in a graphical form on cartesian axes
the optimal waveform profile, the so-called 'cosinorgram' (Fig.10).
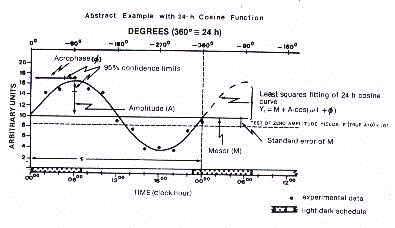
Cosinor procedure additionally expresses both amplitude and
acrophase in polar coordinates within a circle whose 360
sexagesimal degrees correspond to the period of oscillation of
that given bioperiodic event. Such a chronobiologic quadrant is
called 'polargram' (Fig.11).
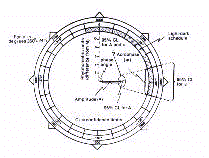
The polargram is a very practical and immediate description of
the cosinor-derived rhythmometric parameters. Amplitude and
acrophase are treated in a bivariate fashion and represented by a
single vector starting from the center. The length of vector is
proportional to the amplitude, while its direction indicates on
the border the temporal localization of acrophase in negative
sexagesimal degrees or in physical time. Importantly, the
polargram allows a bivariate representation of confidence limits
for the amplitude-acrophase pair in form of an ellipse of
confidence centered at the tip of the vector. The confidence
ellipse immediately shows whether or not a rhythm is significant,
respectively by its eccentric or concentric location with
reference to the pole of the circumference. To note that the
statistical limits are given by Single-Cosinor as the standard
error of the mean, and by Population Mean-Cosinor as 95%
confidence limits.
Importance of Cosinor analysis
Cosinor analysis has several fundamental prerequisites with
respect to the macroscopic analysis of temporal series.
The waveform resolution eliminates the spurious or aberrant
data belonging to 'biological noise'. The sinusoidal wave
provides rhythmometric data that are relatively independent from
the density and equidistance of sampled data which is critical in
numerical analysis of raw time data series. Cosinor methodology
has shown that any waveform profile may be defined by only three
parameters, mesor, amplitude and acrophase, which simplify the
description of biologcal rhythms, and, additionally, facilitate
the statistical comparison among oscillating bioevents. As a
matter of fact, the enormous variability of the chronogram makes
the raw data series diffult to be compared and described in their
periodic shape. It must be added that the rhythmometric
parameters provide information on important functional attributes
of oscillating bioevents. The waveform profile, if validated as
significant, demonstrates that the temporal variability of a
given bioevent is systematic and predictable in its periodicity.
The mesor provides an objective measure of the tonic level which
sustains the rhythm. The amplitude, in turn, quantifies the
phasic component which characterizes any oscillating function of
living organisms. Finally, the acrophase estimates the periodic
activity in its best expression.
1.2. Least squares spectral analysis with known periods
This type of analysis is based on the principle of periodic
regression with prefixed periods that are unitary submultiples of
the principal harmonic wave.
This implies that the analysis is linear in period but not in
frequency, exactly the opposite of Fourier analysis.
The formula is
where N is the number of approximated periods and i is the
unitary increment from the lowest period to the period of the
fundamental harmonic. For example, a raw time data series that
covers 24-h can be studied in its harmonic components by
validating whether the periodic regression rejects the null
hypothesis of zero-amplitude at a significant level of
probability (P<0.05) for each fitted period starting from one
cycle per hour to one cycle every 24 hours. In this way, the
unitary harmonic components of the ultraradian and circadian
domain are examined in their amplitude and statistical
significance.
Expressing the extent of oscillation as 'percent rhythm', the
spectrum is given by a cartesian diagram of each amplitude, on
the ordinate, versus each fitted period, on the abscissa, i.e.,
the so called 'power spectrum' (Fig.12).
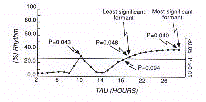
Observing the power spectrum one can immediately decipher the
significant harmonics (formants), including the most significant
(MSH) and the least significant (LSH) one.
Using the formants one can construct a 'harmonic model' of the
signal (Fig.13).
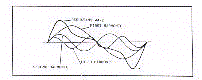
The harmonic model allows the reconstruction of the original
signal, uncontaminated by biological noise, through the
determination of the 'resultant wave' (Fig.14).

1.3. Serial section analysis
This is another method of descriptive inferential
chronobiometry derived from Cosinor analysis. The procedure
consists in iterating the cosine function on a longitudinal
series of biodata that covers a time span longer than one period
of revolution.
Basically, the method applies the Single Cosinor analysis to a
portion of sequential data (serial section) which is included in
the prefixed period of analysis (chronobiological window). The
periodic regression analysis is repeated shifting across a given
number of time data points within the chronobiological window.
The serial section is, therefore, composed of a constant number
of data in each iteration. The analytical approach is progressive,
and ends when the chronobiological window includes the last
portion of data within a complete serial section.
Every iteraction computes the rhythmometric parameters, mesor,
amplitude, acrophase, as well as the percent rhythm and rhythm
detection level. As a consequence, serial section analysis allows
the validation of the significant continuity of rhythmometric
properties over the time in which the sampling was performed (Fig.15).
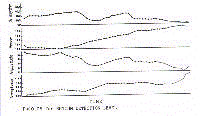
In detail, the analysis estimates whether or not 1. mesor and/or
amplitude tend to vary; 2. acrophase undergoes an anticipatory or
a posticipatory shift as in the presence of free-running or
desynchronizing conditions.
1.4. Multicomponent model of periodic regression analysis
Cosinor analysis may be regarded as an unicomponent model of
periodic regression as it fits a single sinusoidal wave into the
raw time data series.
Some discrete signals in biomedicine are asymmetrical in their
duty-cycle in the sense that they show a different portion of
time in which the measured values fall below and above their mean
level. In this case the best fitting wave is found by periodic
regression models which use more than one harmonic component for
approximating the discrete time data series. The multicomponent
model is usually given by the fundamental wave of period TAU and
N subharmonics, each one (i) having a period TAU(i) that equals
TAU/N.
Therefore, the multicomponent periodic regression analysis is
expressed by the formula
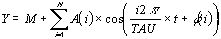
2. Integrative chronobiometry (integrative rhythmometry)
The integrative rhythmometry presently consists in a method
called 'Cosint analysis'.
2.1. Cosint analysis
This procedure is used for estimating bioperiodic events as
integral functions within two temporal limits of their period of
revolution.
The Cosint method consists in a periodic integration analysis
which estimates the area covered by the best fitting waveform
profile of a given biological rhythm. The limits t1 and t2 may be
equal to the period being examined (t2 - t1 = TAU) or to a
fraction of it (t2 - t1 < TAU). Importantly. the cosint
analysis can be performed knowing the periodic regression which
optimally approximates the raw tima data series. Therefore,
Cosint analysis can be applied to cosine models either
unicomponent or multicomponent. In the following example, Cosint
analysis is performed for a sinusoidal curve found by cosinor
analysis (Fig.16).
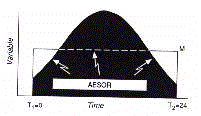
In the other example, Cosint analysis is applied to a profile
found by a two-component model of periodic regression (Fig.17).

The integral over time of the oscillatory curve gives rise to
the parameter aesor (acronym for area estimating statistic of
rhythm).
The aesor is determined from the following formula
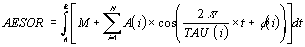
which is suitable for both unicomponent (Cosinor method) and
multicomponent models of periodic regression analysis (see above).
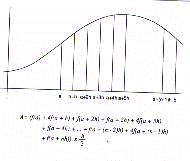
The integral area is calculated by summing the subareas in
which the surface can be divided using as unitary distance the
time base (time unit) corresponding to the period of the
scrutinized rhythm (for example, the minute for circadian rhythms,
the day for circaseptan rhythms, the month for circannual rhythms).
The unitary distance of time corresponds to the h interval. The
subareas are given by quadratic surfaces whose sides correspond
to the two Y values calculated by the periodic regression
function in the h interval of time base (Fig.18).
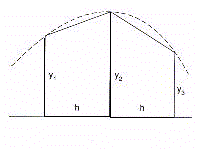
The surface of two contiguous subareas will therefore be given
by the formula
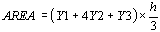
The total area will result from the sum of all the unitary
subareas (Fig.19)
The estimation of total area, aesor, will therefore be given
by the formula
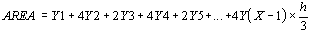
Since the values of Y1, Y2, Y3 ... are given by the periodic
regression function F(Y), the formula can be rewritten as
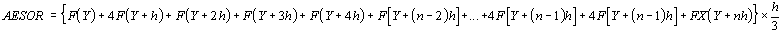
3. Evolutive chronobiometry (evolutive rhythmometry or clinorhythmometry)
The analysis of time-varying cycles may be performed by two
methods which respectively analyze the change in mesor, amplitude
and acrophase, on one side, or period, on the other side.
3.1. Clinospectror analysis
This type of analysis considers the changes of mesor,
amplitude and acrophase (but not period) of biological rhythms
with respect to the chronological age.
So far, the inferential methods which have been discussed
appear to be capable of examinating and describing a rhythmic
bioevent evaluated at a given time of the life cycle. It must be,
however, remarked once again that the majority of biological
rhythms tend to vary in their oscillatory properties with
advancing age. The rhythmometric trend related to chronological
age involves the mesor, amplitude and acrophase (gerorhythmoclinia).
Therefore, there is the need of biometrically investigating such
a complex of changes by means of appropriate procedures (clinorhythmometry).
The approach to age-related changes in rhythmometric parameters
requires a periodic-linear regression analysis in which the trend
in periodic parameters is analyzed as a linear function of age.
Such a method is called 'Clinospectror analysis'. Its formula is
given below
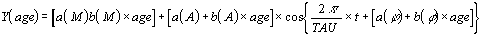
where a is the intercept, i.e., the value of rhythm parameters
at zero age, and b is the angular coefficient of the trend, and M,
A and phi are the rhythmometric parameters, t is a fractional
time of the period in use.
The optimal periodic-linear regression determined by
Clinospectror analysis gives rise to a clinorhythmogram, a
planegraph whose ordinate and abscissa express respectively the
oscillation around the mesor and the chronological age. Examples
of clinorhythmograms are given in figure 2.
According to clinorhythmometry, several models of aging can be
identified as already discussed in previous chapters.
Additionally, Clinospectror analysis may be used for predicting
the evolution of a biological rhythm as a function of life span.
It is possible therefore to make projections to future times as
well as extrapolations to past times down to birth. It is also
possible to predict biological age (BA) with respect to
chronological age (CA), and to compute the senility index (SI)
from the formula SI=BA/CA.
3.2. Complex demodulation method
Biological rhythms may vary in period as a function of
chronological age. The age-related changes in frequency can be
estimated by the model of complex demodulation according to the
following equation

It is important to stress that the chronobiologic methodology
is composed by other procedures for other specific analyses. In
addition, chronobiology uses reference standards which are time-qualified,
i.e., chronodesms, cosinordesms, aesordesms. It is, however,
beyond the informative scope of this article to discuss the
chronobiologic methodology in all its aspects. Readers can find a
stimulus in reviewing the literature cited below if interested in
more details.
CONCLUSIONS
This article is a concise attempt to outline the principles
and methods of chronobiology. Further information will be
provided by the articles which compose this book. These reports
can be regarded as a 'summa chronobiologica' considering that
they have been written by the most distinguished chronobiologists
in the world.
RECOMMENDED BIBLIOGRAPHY
Ajello L. e Fea F. I Bioritmi. Editrice Minerva Medica, 1959.
Arendt J., Minors D.S. and Waterhouse J.M. Biological
Rhythms in Clinical Practice. Wright, London, 1989.
Aschoff J. Zeitgeber der tiorischen Tagesperiodik.
Naturwissenschaften 41: 1954: 49-56.
Aschoff J. und Wever R. Naturwissenschaften 49: 1962: 337-342.
Aschoff J., Daan S. and Groos G. Vertebrate Circadian
Systems: Structures and Physiology. Springer-Verlag, Berlin-Heidelberg-New
York, 1982.
Bingham C., Arbogast B., Cornelissen G., Lee J.K.
and Halberg F. Inferential statistical methods for estimating and
comparing cosinor parameters. Chronobiologia 9: 1984: 397-442.
Biological Rhythms in Clinical and Laboratory Medicine. Y.
Touitou and E. Haus (Eds). Springer-Verlag, Berlin-Heidelberg-
New York, 1992.
Carandente F. Elementi di Cronobiologia Sperimentale e
Clinica. Il Ponte, Milano, 1990.
Chronobiology: Basic and Applied. In: P. Cugini, F. Halberg,
D.W. Wilson and P. Pasquini (Eds). Ann. Istit. Sup. San. Vol. 29.
Istituto Poligrafico e Zecca dello Stato, Roma, 1993, pp. 481-710.
Colquhoun W.P. Aspects of Human Efficiency: Diurnal Rhythms
and Loss of Sleep. English Univ. Press, London, 1972.
Cugini P. Perché la Cronobiologia. La Nuova Critica, 1981,
pp.93-119.
Cugini P. Dynamic rhythmometry: Inferential excess indices
using microcomputers. J. Interdisc. Cycle Res. 18: 1987: 297-306.
Cugini P. Istituzioni di Cronobiologia Medica. Introzzi,
USES Edizioni Scientifiche, 1988, pp. 1729-1806.
Cugini P., Lucia P., Murano G., Di Palma L., Battisti P. e Cogliati A.
Cronobiologia per la medicina: principi e metodologia. Agg. Med.
12: 1988: 675-685.
Cugini P. Chronobiologic Approach to Aging: the
Clinospectroscopic Method. Style Compostampa srl, Roma, 1991.
Cugini P, Di Palma L. Cosint analysis: a procedure for
estimating biological rhythms as integral function by measuring
the area under their best-fitting waveform profile. Biol. Rhythm
Res. 25: 1994: 15-36.
Endocrine Rhythms. D.T. Krieger (Ed). Raven Press, New York,
1979.
Folkard S. and Monk T.H. Hours of Work. John Wiley and Sons,
Chichester, 1985.
Gedda L. e Brenci G. Cronogenetica: L'eredità del Tempo
Biologico. Edizioni Scientifiche e Tecniche, Mondadori, 1974.
Halberg F. Tong Y.L. and Johnson E.A. Circadian system phase:
an aspect of temporal morphology-procedures and illustrative
examples. In: The Cellular Aspects of Biorhythms. Von Mayersbach
H. (Ed). Springer, Berlin 1967, pp. 20-48.
Halberg F., Carandente F, Cornelissen G. and Katinas G.S.
Glossary of Chronobiology. Chronobiologia, 6 (suppl.1): 1977.
Halberg F. I ritmi biologici nella pratica clinica. Minuti 5:
1978: 27-37.
Halberg F., Lee J.K. and Nelson W.L. Time-qualified
reference intervals, chronodesms. Experientia (Basel) 24: 1978:
713-716.
Harris R.G. Biological Clocks. Cold Spring Harbor Symp.
Quant. 1986, pp. 85-113.
Hastinggs J.V. and Schweiger H.G. The Molecular Basis of
Circadian Rhythms. Dahlem Konferenzen, Berlin, 1976.
Hekkens W.Th.J.M., Kerkhof G.A. and Rietveld W.J. Trends in
Chronobiology. Pergamon Press, Oxford, 1988.
Hickey D.S., Kirkland J.L., Lucas S.B. and Lye M. Analysis
of circadian rhythms by fitting a least squares sine curve. Comp.Biol.
Med. 14: 1984: 217-223.
Hildebrandt G. Biologische Rhythmen und Arbeit. Springer-Verlag,
Wien-New York, 1976.
Manfredini R., Gallerani M. e Fersini C. Cronobiologia dell'apparato
cardiovascolare. Editoriale Fernando Folini, Casalnoceto (Alessandria),
1995.
Minors D.S. and Waterhouse J.M. Circadian Rhythms and the
Human. Wright-PSG, Bristol, 1981.
Nelson W., Tong Y.L., Lee K and Halberg F. Methods for
Cosinor-rhythmometry. Chronobiologia 6: 1979: 305-323.
Nelson W., Cornelissen G., Hinkley D., Bingham C. and
Halberg F. Construction of rhythm-specified reference intervals
and regions, with emphasis on 'hybrid' data, illustrated for
plasma cortisol. Chronobiologia 10: 1983: 179-193.
Nicholson A.N. Sleep, Wakefullness and Circadian Rhythm.
AGARD Lecture Series No. 105, 1979.
Orologi Biologici. Le Science. (Quaderni) 9: 1983: 2-79.
Palmer J.D., Brown F.A.Jr. and Edmunds L.N. Introduction of
Biological Rhythms. Academic Press, New York, 1976.
Redfern P.H., Campbell I.C., Davies J.A. and Martin K.F.
Circadian Rhythms in the Central Nervous System. MacMillan Press
LTD., London, 1985.
Reinberg A. Dai Ritmi Biologici alla Cronobiologia. I
Quaderni de 'Il Ponte'. Chronobiologia (Suppl.2): 1975: 7-97.
Rietveld W.J. Clinical Aspects of Chronobiology. Meducation
Service Hoechst, 1986.
Sanchez De La Pena S., Halberg F., Halberg E., Ungar F.,
Cornelissen G., Sanchez E., Brown G., Scheving L.E., Yunis E.G.
and Vecsei P. Pineal Modulation of ACTH 1-17 Effect upon Murine
Corticosterone Production. Brain Research Bulletin 11: 1983: 117-125.
Sensi S. Elementi di Cronobiologia Clinica. Esculapio Ed.,
Bologna, 1984.
Tarquini B. Cronobiologia Pratica. Esculapio Ed., Bologna,
1984.
Timing and Time Perception. J. Gibbon and L. Allan (Eds).
Ann. N.Y. Acad. Sci. 423: 1984.
 Utilizing Clinospectror analysis (see below), both positive
and negative trends (clinous) have been identified for mesor and
amplitude as an effect of age (Fig.2).
Utilizing Clinospectror analysis (see below), both positive
and negative trends (clinous) have been identified for mesor and
amplitude as an effect of age (Fig.2).
 Therefore there are 'dianaclinous' or 'dikataclinous' rhythms
if both properties have a positive or negative trend during the
course of life. Rhythms can also be defined as 'mesor-anaclinous'
or 'mesor-kataclinous', and 'amplitude-anaclinous' or 'amplitude-kataclinous',
if the evolution through chronological time involves only one of
the parameters in either a positive or negative sense. There is
also the possibility of a trend opposite to the two rhythmic
properties defined as an 'amphiclinous' rhythm. Finally, there
can be an 'aclinous' rhythm which is a rhythm that shows itself
to be stable even though the age increases.
Therefore there are 'dianaclinous' or 'dikataclinous' rhythms
if both properties have a positive or negative trend during the
course of life. Rhythms can also be defined as 'mesor-anaclinous'
or 'mesor-kataclinous', and 'amplitude-anaclinous' or 'amplitude-kataclinous',
if the evolution through chronological time involves only one of
the parameters in either a positive or negative sense. There is
also the possibility of a trend opposite to the two rhythmic
properties defined as an 'amphiclinous' rhythm. Finally, there
can be an 'aclinous' rhythm which is a rhythm that shows itself
to be stable even though the age increases.
 Chronobiology considers aging in the context of cyclicity
which characterizes biological functions. Studies done in this
regard have demonstrated that senescence is associated with a
decline which affects the mean level (gerontologic decline of
tonic activity), and the extent (gerontologic decline of phasic
activity) of oscillation, as well as a shift in the phase (gerontologic
rephasement) and/or a change in the period (gerontologic
demultiplication/multiplication) of biological rhythms.
Accordingly, it can be said that aging is a process associated
with a trend (clinous) which is negative for height and
oscillatory extent of bioperiodic functions. This implies that
the effects of senescence consist in a model of periodic-linear
regression, in which one can see the combined decline of the
oscillation in its mean level and amplitude, i.e., a phenomenon
of gerorhythmoclinia (Fig.4).
Chronobiology considers aging in the context of cyclicity
which characterizes biological functions. Studies done in this
regard have demonstrated that senescence is associated with a
decline which affects the mean level (gerontologic decline of
tonic activity), and the extent (gerontologic decline of phasic
activity) of oscillation, as well as a shift in the phase (gerontologic
rephasement) and/or a change in the period (gerontologic
demultiplication/multiplication) of biological rhythms.
Accordingly, it can be said that aging is a process associated
with a trend (clinous) which is negative for height and
oscillatory extent of bioperiodic functions. This implies that
the effects of senescence consist in a model of periodic-linear
regression, in which one can see the combined decline of the
oscillation in its mean level and amplitude, i.e., a phenomenon
of gerorhythmoclinia (Fig.4).
 Presently, the periodic-linear regression analysis of
gerontological trends of biological rhythms is feasible by means
of the Clinospectror method. This procedure, developed by this
author, combines the estimation of the oscillatory changes,
period by period, as a function of linear advancing age. The
model of the gerontological destiny of biological rhythms is
represented by a curve, i.e., the gerorhythmoclinogram (Fig.2).
Interestingly, the clinorhythmometric study of senescence has
documented that some biological rhythms may show a decline (kataclinous
rhythms or katarhythms), some others may exhibit an amplification
(anaclinous rhythms or anarhythms), in either the mean or
amplitude of oscillation, and, finally, some others may appear
not to change at all (aclinous rhythms or isorhythms), with
advancing age. The gerorhythmoclinograms of these trends have
been already illustrated in figure 2.
The kataclinous trend is a typical expression of rhythms 'causative'
of senescence. The anaclinous trend, by contrast, represents the
periodic-linear model of rhythms 'adaptive' to aging.
Presently, the periodic-linear regression analysis of
gerontological trends of biological rhythms is feasible by means
of the Clinospectror method. This procedure, developed by this
author, combines the estimation of the oscillatory changes,
period by period, as a function of linear advancing age. The
model of the gerontological destiny of biological rhythms is
represented by a curve, i.e., the gerorhythmoclinogram (Fig.2).
Interestingly, the clinorhythmometric study of senescence has
documented that some biological rhythms may show a decline (kataclinous
rhythms or katarhythms), some others may exhibit an amplification
(anaclinous rhythms or anarhythms), in either the mean or
amplitude of oscillation, and, finally, some others may appear
not to change at all (aclinous rhythms or isorhythms), with
advancing age. The gerorhythmoclinograms of these trends have
been already illustrated in figure 2.
The kataclinous trend is a typical expression of rhythms 'causative'
of senescence. The anaclinous trend, by contrast, represents the
periodic-linear model of rhythms 'adaptive' to aging.
 In the discretization of bioperiodic phenomena there is the
risk of systematic errors, any temporal series being constituted
by an intrinsic component which is superimposed by occasional or
random elements. The discrete series can, therefore, be
contaminated by aberrant values, the so called 'biological noise',
not belonging to the systematic component of the periodic
variation (Fig.6).
In the discretization of bioperiodic phenomena there is the
risk of systematic errors, any temporal series being constituted
by an intrinsic component which is superimposed by occasional or
random elements. The discrete series can, therefore, be
contaminated by aberrant values, the so called 'biological noise',
not belonging to the systematic component of the periodic
variation (Fig.6).
 In order to remove the biological noise
due to aberrant values, the so called 'outliers', the periodic
signal has to be geometrically approximated by a curve adjusted
to the raw series of data (Fig.7).
In order to remove the biological noise
due to aberrant values, the so called 'outliers', the periodic
signal has to be geometrically approximated by a curve adjusted
to the raw series of data (Fig.7).
 As the signal is periodic, the analytical curve has to be
representative of the harmonic oscillation. Therefore, one can
assume that a biological rhythm is better expressed by the
oscillating wave which optimally fits the discrete signal in its
periodic fluctuation. In line with this thought, one can suggest
that a biological rhythm is by definition 'the periodic component
of a temporal series of biological data whose waveform profile
has been analytically validated'. In other words, a biological
rhythm is 'a biosignal whose period of oscillation has been
validated by analytical models of periodic regression using one
or more harmonic components'. Assuming such a definition, one can
argue that a discrete variation of temporal biodata is not
implicitly a pattern demonstrating a biological rhythm. Obviously,
the analytical resolution of a discrete biosignal doesn't imply
that the biological rhythm is arranged in a perfect sinusoidal
shape. The sinusoidalization is just a model for removing the
aleatory components which causes biological noise and, thus,
biometric disturbance.
Furthermore, there are other valid biostatistical reasons that
recognize the harmonic representation as the ideal signal of
biological cycles. As a variation occurring over the 24-h scale
is not an implicit demonstration that the pattern varies
according to a 24-h period, there is the need to statistically
validate the oscillation in its periodicity. The rhythm detection
level may be statistically verified assuming an 'alpha'
probability (P) of less than 5% for the null-hypothesis of non-oscillation
(zero-amplitude). Using the harmonic model, the biological
rhythmicity may be, thus, statistically validated in its
significance against the probability of P<0.05 that the extent
of oscillation is due to the effect of randomness.
The periodic regression methods used in the analytical
detection and sinusoidal testing of discrete time series of
biodata are discussed in the following chapter.
As the signal is periodic, the analytical curve has to be
representative of the harmonic oscillation. Therefore, one can
assume that a biological rhythm is better expressed by the
oscillating wave which optimally fits the discrete signal in its
periodic fluctuation. In line with this thought, one can suggest
that a biological rhythm is by definition 'the periodic component
of a temporal series of biological data whose waveform profile
has been analytically validated'. In other words, a biological
rhythm is 'a biosignal whose period of oscillation has been
validated by analytical models of periodic regression using one
or more harmonic components'. Assuming such a definition, one can
argue that a discrete variation of temporal biodata is not
implicitly a pattern demonstrating a biological rhythm. Obviously,
the analytical resolution of a discrete biosignal doesn't imply
that the biological rhythm is arranged in a perfect sinusoidal
shape. The sinusoidalization is just a model for removing the
aleatory components which causes biological noise and, thus,
biometric disturbance.
Furthermore, there are other valid biostatistical reasons that
recognize the harmonic representation as the ideal signal of
biological cycles. As a variation occurring over the 24-h scale
is not an implicit demonstration that the pattern varies
according to a 24-h period, there is the need to statistically
validate the oscillation in its periodicity. The rhythm detection
level may be statistically verified assuming an 'alpha'
probability (P) of less than 5% for the null-hypothesis of non-oscillation
(zero-amplitude). Using the harmonic model, the biological
rhythmicity may be, thus, statistically validated in its
significance against the probability of P<0.05 that the extent
of oscillation is due to the effect of randomness.
The periodic regression methods used in the analytical
detection and sinusoidal testing of discrete time series of
biodata are discussed in the following chapter.
 The within-day profile of mean values that results from this
analysis may be called the 'chronogram'. Importantly, in each
point the dispersion around the mean may be measured in terms of
standard deviation (SD), standard error of the mean (SE or SEM),
or 95% confidence limits (95%CL).
The true effect of time on temporal distribution of data may
be ascertained by means of the 'one-way variance analysis' (one-way
ANOVA). The homogeneity of variance in each time point (homoschedasticity)
may be verified by means of Bartlett's test or Duncan's test.
The estimates on the chronograms are as follows: 1. overall
mean level; 2. peak level; 3. peak time (zenith); 4. trough level;
5. trough time (nadir); 6. difference between peak and trough
levels; 7. coefficient of variation for time-qualified mean
levels.
The within-day profile of mean values that results from this
analysis may be called the 'chronogram'. Importantly, in each
point the dispersion around the mean may be measured in terms of
standard deviation (SD), standard error of the mean (SE or SEM),
or 95% confidence limits (95%CL).
The true effect of time on temporal distribution of data may
be ascertained by means of the 'one-way variance analysis' (one-way
ANOVA). The homogeneity of variance in each time point (homoschedasticity)
may be verified by means of Bartlett's test or Duncan's test.
The estimates on the chronograms are as follows: 1. overall
mean level; 2. peak level; 3. peak time (zenith); 4. trough level;
5. trough time (nadir); 6. difference between peak and trough
levels; 7. coefficient of variation for time-qualified mean
levels.
 Assuming the periode of revolution to be equal to TAU, the
formula for spectral analysis can be rewritten
Assuming the periode of revolution to be equal to TAU, the
formula for spectral analysis can be rewritten
 Cosinor procedure additionally expresses both amplitude and
acrophase in polar coordinates within a circle whose 360
sexagesimal degrees correspond to the period of oscillation of
that given bioperiodic event. Such a chronobiologic quadrant is
called 'polargram' (Fig.11).
Cosinor procedure additionally expresses both amplitude and
acrophase in polar coordinates within a circle whose 360
sexagesimal degrees correspond to the period of oscillation of
that given bioperiodic event. Such a chronobiologic quadrant is
called 'polargram' (Fig.11).
 The polargram is a very practical and immediate description of
the cosinor-derived rhythmometric parameters. Amplitude and
acrophase are treated in a bivariate fashion and represented by a
single vector starting from the center. The length of vector is
proportional to the amplitude, while its direction indicates on
the border the temporal localization of acrophase in negative
sexagesimal degrees or in physical time. Importantly, the
polargram allows a bivariate representation of confidence limits
for the amplitude-acrophase pair in form of an ellipse of
confidence centered at the tip of the vector. The confidence
ellipse immediately shows whether or not a rhythm is significant,
respectively by its eccentric or concentric location with
reference to the pole of the circumference. To note that the
statistical limits are given by Single-Cosinor as the standard
error of the mean, and by Population Mean-Cosinor as 95%
confidence limits.
The polargram is a very practical and immediate description of
the cosinor-derived rhythmometric parameters. Amplitude and
acrophase are treated in a bivariate fashion and represented by a
single vector starting from the center. The length of vector is
proportional to the amplitude, while its direction indicates on
the border the temporal localization of acrophase in negative
sexagesimal degrees or in physical time. Importantly, the
polargram allows a bivariate representation of confidence limits
for the amplitude-acrophase pair in form of an ellipse of
confidence centered at the tip of the vector. The confidence
ellipse immediately shows whether or not a rhythm is significant,
respectively by its eccentric or concentric location with
reference to the pole of the circumference. To note that the
statistical limits are given by Single-Cosinor as the standard
error of the mean, and by Population Mean-Cosinor as 95%
confidence limits.
 Observing the power spectrum one can immediately decipher the
significant harmonics (formants), including the most significant
(MSH) and the least significant (LSH) one.
Using the formants one can construct a 'harmonic model' of the
signal (Fig.13).
Observing the power spectrum one can immediately decipher the
significant harmonics (formants), including the most significant
(MSH) and the least significant (LSH) one.
Using the formants one can construct a 'harmonic model' of the
signal (Fig.13).
 The harmonic model allows the reconstruction of the original
signal, uncontaminated by biological noise, through the
determination of the 'resultant wave' (Fig.14).
The harmonic model allows the reconstruction of the original
signal, uncontaminated by biological noise, through the
determination of the 'resultant wave' (Fig.14).

 In detail, the analysis estimates whether or not 1. mesor and/or
amplitude tend to vary; 2. acrophase undergoes an anticipatory or
a posticipatory shift as in the presence of free-running or
desynchronizing conditions.
In detail, the analysis estimates whether or not 1. mesor and/or
amplitude tend to vary; 2. acrophase undergoes an anticipatory or
a posticipatory shift as in the presence of free-running or
desynchronizing conditions.
 In the other example, Cosint analysis is applied to a profile
found by a two-component model of periodic regression (Fig.17).
In the other example, Cosint analysis is applied to a profile
found by a two-component model of periodic regression (Fig.17).
 The integral over time of the oscillatory curve gives rise to
the parameter aesor (acronym for area estimating statistic of
rhythm).
The aesor is determined from the following formula
The integral over time of the oscillatory curve gives rise to
the parameter aesor (acronym for area estimating statistic of
rhythm).
The aesor is determined from the following formula
 The surface of two contiguous subareas will therefore be given
by the formula
The surface of two contiguous subareas will therefore be given
by the formula
 The estimation of total area, aesor, will therefore be given
by the formula
The estimation of total area, aesor, will therefore be given
by the formula